Mamba是从selective state space model改进而来的,与其类似的还有LSTM以及NTM。LSTM的问题在于forget gate和input gate都依赖于$cat[h_{t-1}, x_t]$,于是完全无法sequence并行。NTM的controller也有类似的问题,于是二者训练时速度都很慢,无法按照scaling law扩展下去。Mamba保留了推理时自回归state,使state不随时间L扩张size的的特性同时,也允许训练时以$O(ln(L))$复杂度进行reduce,之后进行并行计算。再加上充分进行了cuda kernel的访存优化,使其在短文本训练时速度可以与transformer架构对比,同时避免了在长文本时以transformer结构的$O(L^2)$计算复杂度进行推理,是比较适合超长文本的一种模型。
Mamba的数学细节如下:
state $h(t)$被视作时间连续状态,一阶时间导使用神经网络进行建模。$h'(t) = \boldsymbol{A} h(t) + \boldsymbol{B} x(t)$。则在小增量$\Delta$时,$h_{t+1}-h_t \approx \Delta \left( \boldsymbol{A}h_t + \boldsymbol{B} x_t \right)$
于是得到$h_{t+1} \approx (\boldsymbol{I} + \Delta \boldsymbol{A})h_t + (\Delta \boldsymbol{B}) x_t$。注意这里的$\Delta$与后面的矩阵并非matmul,而是elementwise multiply。矩阵与向量$h$也并非矩阵乘法,而是unsqueeze, repeat之后再elementwise multiply。
上面$\boldsymbol{I}$和$\boldsymbol{A}$都与x无关,所以要合理地对第一项代表了“梯度”的部分进行建模,需要让步长$\Delta(x)$依赖于x。这种基于极限微分的离散化方法比较简单,但不够稳定和精确,于是论文中使用了zero-order hold方法进行离散化。
我们知道满足$\frac{dh(t)}{dt} = \boldsymbol{A} h(t) + \boldsymbol{B} x(t)$的函数解包括了$h(t) = e^{\boldsymbol{A}(t-t_0)}h(t_0) + \int_{\tau=t_0}^{t} e^{\boldsymbol{A}(t-\tau)} \boldsymbol{B} x(\tau) d\tau$
证明:令$t_0=0$,评估$\tau=t$时的梯度
第二项积分求导$=e^{\boldsymbol{A}(t-t)}\boldsymbol{B} x(t)=\boldsymbol{B} x(t)$
第一项求导=$\boldsymbol{A} e^{\boldsymbol{A} t}h(t_0) = \boldsymbol{A} h(t)$
注意上面的$\boldsymbol{A}(t-t_0)$并非表示$\boldsymbol{A}$是t的函数,而是表示元素乘积,即$(t-t_0)\boldsymbol{A} = \boldsymbol{A}(t-t_0)$
接下来考虑从0到t中间的单个step:$t_{k+1}-t_k = \Delta$,代入解方程,得到
$h_{k+1} = e^{\boldsymbol{A} \Delta} h_k + \int_{\tau=t_k}^{t_{k+1}} e^{\boldsymbol{A} (t_{k+1} – \tau)} \boldsymbol{B} x_k d\tau$
这里$x(\tau)$局部离散化变成了$x_k$,可以和$\boldsymbol{B}$一起放到积分外面。
于是可以重新定义$\bar{\boldsymbol{A}}$与$\bar{\boldsymbol{B}}$,使$h_{k+1}$回到线代的计算方式。
$\bar{\boldsymbol{A}} = exp(\boldsymbol{A} \Delta)$
$\bar{\boldsymbol{B}} = \int_{\tau=0}^{\Delta} e^{\boldsymbol{A} \tau} d\tau \boldsymbol{B} = \frac{1}{ \Delta \boldsymbol{A}} \left( exp(\Delta \boldsymbol{A} – \boldsymbol{I} ) \right) \cdot \Delta \boldsymbol{B}$
$\bar{\boldsymbol{B}}$里面的identity matrix来自积分下界在每一步重新定义的原点的评估,于是论文中的zero-order holder离散化公式推导完成。
最终$h_{k+1} = \bar{\boldsymbol{A}} h_{k} + \bar{\boldsymbol{B}} x_k $。为了使其更接近RNN的自回归样式,需要重新定义下标,以及$x_k$的离散化位置。
重写为论文中的$h_{t} = \bar{\boldsymbol{A}} h_{t-1} + \bar{\boldsymbol{B}} x_t$
mamba允许步长$\Delta$被x参数化,$\bar{\boldsymbol{A}}=exp(\Delta(x) \boldsymbol{A})$,工程上为了让$\bar{\boldsymbol{A}}$的响应对训练参数更敏感且不会exp爆炸,会再进行一次重参数化操作:$\boldsymbol{A}=-exp(\boldsymbol{A}_{log})$,其中$\boldsymbol{A}_{log}$是叶子节点可训练参数。这个细节并非论文中提到的,而是工程代码中的实现。
论文中$\Delta(x)=softplus(P_{\Delta} + Linear(x))$,但代码实现里是$\Delta(x)=softplus \left( Linear_{bias=P_{\Delta}}\left(Linear(x)\right) \right)$的做法,增加了一个可训练矩阵乘法参数,然后将原本的参数合入新linear层的bias中。
这些重参数化方法最终都确保了softplus得到的$\Delta(x) \ge 0$,同时$\boldsymbol{A} \le 0$,于是二者相乘再取exp,获得的$\bar{\boldsymbol{A}} \le 1$,即forget gate不大于1。
使用softplus作为$\Delta(x)$的重参数激活,也可以看作是对gate机制的一种泛化。考虑当-torch.ones填充的$\boldsymbol{A}=-1$,torch.ones填充$\boldsymbol{B}=1$时,$\bar{\boldsymbol{A}}$可以表示为:
$\bar{\boldsymbol{A}} = exp(\Delta \boldsymbol{A}) = exp\left( -1 \cdot log \left( 1 + exp(Linear^2(x)) \right) \right)$
$= sigmoid(-Linear^2(x)) = 1-sigmoid(Linear^2(x))$
这时$\bar{\boldsymbol{A}}$变成了LSTM里的那种sigmoid forget gate。
同时$\bar{\boldsymbol{B}} = \frac{1}{ \Delta \boldsymbol{A}} \left( exp(\Delta \boldsymbol{A} – \boldsymbol{I} ) \right) \cdot \Delta \boldsymbol{B} = -exp(\Delta \boldsymbol{A} – \boldsymbol{I}) = 1- \bar{\boldsymbol{A}} = sigmoid(Linear^2(x))$
于是在A=-1,B=1的特定条件下,Selective SSM的选择机制退化成为sigmoid gate:$h_{t} = (1-g_t) h_{t-1} + g_t x_t$,where $g_t=g(x_t)=\text{sigmoid gate}$
最后output gate $\boldsymbol{C}$就很简单了,$y_{t}=\boldsymbol{C} h_t$
要解决$h_t$依赖于$h_{t-1}$导致类似RNN一样无法并行的问题,就需要针对$h_t$进行一些递推展开:
$h_0 = \bar{\boldsymbol{B}} x_0$
$h_1 = \bar{\boldsymbol{A}} h_0 + \bar{\boldsymbol{B}} x_1 = \bar{\boldsymbol{A}} \bar{\boldsymbol{B}} x_0 + \bar{\boldsymbol{B}} x_1$
$h_T= \sum_{t=0}^{T} \bar{\boldsymbol{A}}^t \bar{\boldsymbol{B}} x_t $
以及
$y_T = \sum_{t=0}^{T} \bar{\boldsymbol{C}} \bar{\boldsymbol{A}}^t \bar{\boldsymbol{B}} x_t $
通过$\boldsymbol{A}$的连乘,能够让$h_t$与$h_{t-1}$相互解耦,但如果要用for循环t次来计算${\boldsymbol{A}}$,速度是一样慢的,都需要$O(T)$,甚至因为比较多的重复A乘计算,开销会更大。
于是需要使用一个技巧,叫Blelloch Scan,简单举例如下:
假设我们需要累加从1到8,数组position从1开始到8结束,数值等于position只是方便说明,实际上可换成任意数字。
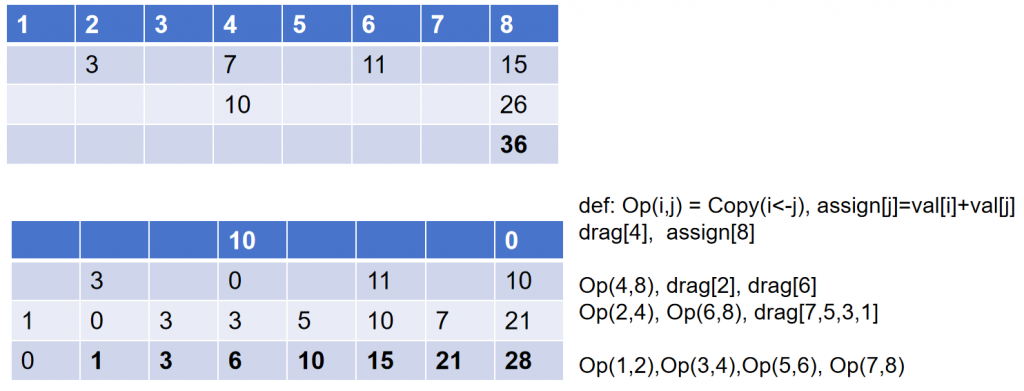
首先需要确保长度是2整数幂,之后二分法用$O(ln(T))$代价求前缀和,得到上半部分的倒三角型,需要把这个三角形的结果缓存,后面会用到。
上层倒三角的右下方36是整个序列的和。之后开始填写下面的数组,规则如下:
- 从最大T/2的间隔开始,drag代表从上层三角矩阵里拖拽对应位置的数值到下面的table,assign代表直接赋值。
- 首先drag位置4的值10,之后assign位置8的数值0。
- 之后定义operator $Op(i,j) = copy(i \leftarrow j) \& assign(j, val[i]+val[j])$,左右两个position的数值,右侧赋值给左侧,同时右侧赋值为两个位置的数值和。
- Op(4,8)执行之前准备好的4和8位置上的数,同时drag[2, 6]两个位置的数(上次drag了1个位置,这次drag位置数量翻倍)
- 目前位置2,4,6,8的数值就绪,可以继续按照二分法的分组规律,两两执行Op(i,j)操作。同时还可以drag[1,3,5,7]这四个位置的数值。
- 最终4组Op(i,j)运算过后,得到正确的前缀和序列,用粗体标识。
这样总计算步骤就从$O(T)$减少为$2 O(ln(T))$,能够在GPU上进行并行加速。
Mamba设计的算法比较巧妙,将所有copy和drag的操作都隐藏到了流处理器的高速shared memory里,这样访存很慢的global memory只需要在算子输入和输出进行两次读写,就可以完成上面的计算。
虽然计算的是累乘,而非样例中的累加,但原理是一样的。
这种parallel scan只能在训练时使用,且反向传播时pscan层无法缓存所有activation,没有activation checkpoint只能重新计算,不过好在shared memory里计算成本不算高。
推理时逐个generator就无法使用pscan模式了,有另一个基于cache版本的$h_{t}$算法。
以上描述的都是ssm模块,而完整的mamba模块,是下图最右侧的样子,还多了一些控制单元,residual和projection。再外层就与transformers没有太大差别了。
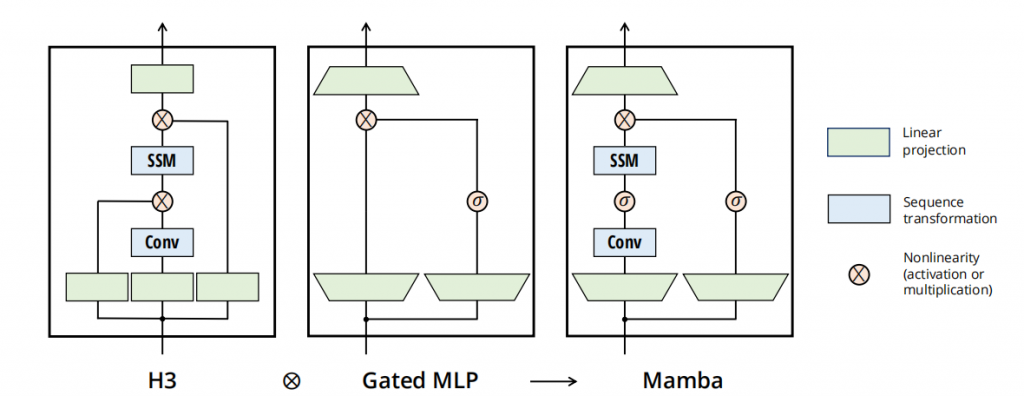
Jamba模型在mamba block里面添加了带moe的mlp层,同时混合使用了transformer block以及mamba block,取得了不错的效果。
感兴趣可以阅读一下《Jamba: A Hybrid Transformer-Mamba Language Model 》这篇。
总结:
Mamba就是将一个比较通用的SSSM模型,改造成了不依赖于横向的$h_{t-1}$,而只依赖于纵向$x_{0:t}$的某种累乘的形式,从而绕开了RNN自回归在训练时的性能瓶颈。同时这种累乘还能够被parallel scan一定程度上并行处理,于是可以放入GPU的cuda核心进行加速。再结合一些shared memory的优化技巧,使全局显存的访存消耗降低,提升性能。
