使用优势函数进行策略梯度的方法,需要先计算梯度
$g = \mathbb{E}_{p(s,a,k) \sim \tau} \left[ A(s, a) \nabla_{\theta}(log \pi(a \mid s)) \right]$
其中$A(s, a)$需要以某种形式直接或是间接由critic网络给出。暂时不考虑critic的拟合与优化,$\tau$的获取方式需要某种actor策略$\pi_{traj}$。这个策略与需要更新训练的$\pi(a \mid s)$有可能是同样的(on policy),也可能有不同(off policy)。
策略梯度需要一个步长超参,然而在比较陡峭的Loss平面上,步长很难决定。
策略梯度的优化最终目标都是$J = \mathbb{E}_{s_0 \sim p(s_0)}[V_{\pi}(s_o)]$,考虑一次策略的更新$ \pi_{old}(\theta_{old}) \rightarrow \pi_{new}(\theta_{new})$,由于步长的问题,无法保证每次按照$\nabla_{\theta}J$方向更新时,J都能增加。所以尝试找到一种方法,使得$J(\pi) = J(\pi_{old}) + something$能够一直增加。
1. 问题转化
首先需要完成一个看似无意义的问题转化,转化后方便进行后续几个优化操作。
考虑$A_{\pi_{old}}(s, a)=Q(s, a) – V(s) = Q(s, a)-\sum\limits_{a’ \sim \pi_{old}} \pi_{old}(a’ \mid s) Q(s, a’)$
1步td时存在$A_{\pi_{old}}(s, a)= \mathbb{E}_{s’} \left[ R_{s \rightarrow s’}^{a \sim \pi_{old}} + \gamma V_{\pi_{old}}(s’) – V_{\pi_{old}}(s) \right]$
则当采样是从新策略$\tau \mid \pi$获得的trajectory时
$\mathbb{E}_{s_0,a_0,… \mid \pi} \left[ \sum\limits_{t=0}^{\infty} \gamma^t A_{\pi_{old}}(s_t, a_t) \right]= \mathbb{E}_{s \sim \tau_{new}} \left[ \sum\limits_{t=0}^{\infty} \gamma^t r(s_t) \right] + \mathbb{E}_{s_0 \sim \tau?} \left[ -V_{\pi_{old}}(s_0) \right]$
这里第二项中的预期,无论$\tau \mid \pi$还是$\tau \mid \pi_{old}$,起点$s_0$都是一样的,而第一项的reward需要从$\tau \mid pi$新策略的trajectory里累积。而第一项又正好符合定义$\mathbb{E}_{s_0}[V_{\pi}(s_0)]=J(\pi)$,所以
$J(\pi) – J(\pi_{old}) = \mathbb{E}_{\tau \mid \pi} \left[ \sum\limits_{t=0}^{\infty} \gamma^t A_{\pi_{old}}(s_t, a_t) \right]$
重写一下得到
$J(\pi) = J(\pi_{old}) + \mathbb{E}_{\tau \mid \pi} \left[ \sum\limits_{t=0}^{\infty} \gamma^t A_{\pi_{old}}(s_t, a_t) \right]$
要评估右边的预期值括号时,就出现了一个问题:1步td的$A_{\pi_{old}}(s, a)$使用到的状态转移来计算$V(s’)$和$V(s)$时,要依赖于旧策略$\pi_{old}$,然而在$\sum\limits_{t=0}^{\infty}$时,又需要t在新策略$\pi$生成的trajectory上推进。这让该项变得难以评估。
于是退一步,让sum的trajectory也使用$\pi_{old}$,其他地方维持不变,就定义了一个新的东西,作为$J(\pi)$的某种近似,叫做替代函数surrogate function:
$L_{\pi_{old}}(\pi) = J(\pi_{old}) + \mathbb{E}_{\tau \mid \pi_{old}} \left[ \sum\limits_{t=0}^{\infty} \gamma^t A_{\pi_{old}}(s_t, a_t) \right]$
这个函数我们可以方便地按照正常的方式采样计算,但是它和我们的最终目标$J(\pi)$仍然存在区别。这个区别要怎样评估呢?
首先,$A_{\pi_{old}}(s, a)$可正可负,当$a$因为新旧$\pi(a \mid s)$导致的差异而改变时,优势函数的最大误差不会超过
$$2 \mathop{\max}_{s, a} | A_{\pi_{old}}(s, a)|$$
假设$P(a_{\pi} \neq a_{\pi_{old}}) \le \alpha$,即两种策略得出的action不同的概率存在一个最大值$\alpha$
那么每一步的优势函数的误差,定义为左边,满足$$|\bar{A}(s)| \le 2 \alpha \mathop{\max}_{s, a} | A_{\pi_{old}}(s, a)| $$
有了一条路径上的单步误差上限,那么当计算$J(\pi) – L_{\pi_{old}}(\pi)$,涉及到两条路径时,
$\mathbb{E}_{\tau \mid \pi} […] – \mathbb{E}_{\tau \mid \pi_{old}} […]$两个预期括号内的单步总误差,最坏情况就是
$|\bar{A}(s \sim \tau_{\pi}) – \bar{A}(s \sim \tau_{\pi_{old}})| \le |\bar{A}(s \sim \tau_{\pi})| + | \bar{A}(s \sim \tau_{\pi_{old}})| = 4 \alpha \mathop{\max}_{s, a} | A_{\pi_{old}}(s, a)|$
为了方便,定义$\epsilon :=\mathop{\max}_{s, a} | A_{\pi_{old}}(s, a)| $
定义$n_t$是在某条路径上,截至到第t步之前的所有时间i,$a_i^{(\pi)} \neq a_i^{(\pi_{old})}$的次数,则有
$P(n_t=0) \ge (1-\alpha)^t$,以及$P(n_t > 0) \le 1 – (1-\alpha)^t$
对于任意一条路径,存在$\mathbb{E}_{\tau \mid pi?}[…] = P(n_t=0) \mathbb{E}_{\tau \mid pi?, n_t=0}[…] + P(n_t>0) \mathbb{E}_{\tau \mid pi?, n_t>0}[…]$
其中第一项$n_t=0$意味着新旧策略路径一样(截至到t时),括号内的优势函数也一样,所以可以完全抵消,只剩$n_t>0$的部分。
所以$|J(\pi) – L_{\pi_{old}}(\pi)| \le \sum\limits_{t}^{\infty} \gamma^t P(n_t>0) 4 \alpha \epsilon$
$ = 4 \epsilon \alpha \left( \sum\limits_{t=0}^{\infty}\gamma^t – \sum\limits_{t=0}^{\infty}(1-\alpha)^t \right)$
$ =\frac{4 \epsilon \alpha^2 \gamma } {(1-\gamma)[1 – \gamma(1-\alpha)]}$
$\le \frac{4 \epsilon \alpha^2 \gamma } {(1-\gamma)^2} $
注意到$\alpha$实际上就是将$\pi$与$\pi_{old}$在每一种操作上产生不一样的结果的概率加起来,得到单步错误的概率,再取所有步数内的最大错误概率,即$$ \alpha = \mathop{\max}_{s_t \sim \tau?} D_{TV}(\pi(\cdot \mid s_t) || \pi_{old}(\cdot \mid s_t))$$
这里对于tv距离的使用,因为对称性所以在哪种策略使用的路径上计算,都是可用的。
然后利用不等式$D_{TV}(p || q)^2 \le D_{KL}(p || q)$
可得 $J(\pi) \ge L_{\pi_{old}}(\pi) – \frac{4 \epsilon \gamma}{(1-\gamma)^2} D_{KL}^{max_{s \sim \tau_{old}}}(\pi_{old} || \pi) := M(\pi)$
接下来试着把$\pi = \pi_{old}$的情况带入,分析
$L(\pi=\pi_{old})= J(\pi_{old}) + \sum\limits_{s \sim \tau \mid \pi_{old}} \rho(s) \sum\limits_{a} \pi(a \mid s, \theta=\theta_{old}) A_{\pi_{old}}(s, a))$
根据优势函数的定义,右边第二项里$\sum_a$的操作,会使得右侧的预期值为0,结果就是让$L(\pi(\theta_0))=J(\pi(\theta_0))$
此时KL距离也是0,导致$M(\pi=\pi_{old}) = J(\pi_{old})$
所以每次从$\pi_{old}$更新到$\pi$,只要优化$M$,就能确保$J$的增量不会少于M的增量,由此证明训练问题可以转化。
2. 模型主要思想
在考虑优化M的问题之前,可以把$M(\pi)$看作是优化$L_{\pi_{old}}(\pi)$的同时,使用惩罚项$$\mathop{\max}_{s_t \sim \tau_{old}} D_{KL}[\pi_{old}(\cdot \mid s_t) || \pi(\cdot \mid s_t)]$$以及惩罚系数$C=\frac{4 \epsilon \gamma}{(1-\gamma)^2} $
直接使用这个惩罚系数的话,因为它很大,会导致步长太小,收敛太慢,所以放宽惩罚,改用约束条件,即:
优化$L_{\pi_{old}}(\pi)$的同时,要求$D_{KL}^{max_{s \sim \tau_{old}}}(\pi_{old} || \pi) \le \delta$
$L_{\pi_{old}}(\pi) = J(\pi_{old}) + \sum\limits_{s \sim \tau \mid \pi_{old}} \rho(s) \sum\limits_{a} \pi(a \mid s, \theta) A_{\pi_{old}}(s, a))$
为了能让第二项在$\tau \mid \pi_{old}$内使用旧策略采样,与需要进行更新训练的策略(即与优势函数相乘的策略)允许存在一些差距(off policy),于是使用importance sample方法,L的第二项修改为:
$\mathbb{E}_{s, a \sim \tau \mid \pi_{old}} \left[ \frac{\pi(a \mid s, \theta)}{\pi(a \mid s, \theta_{old}) } A_{\pi_{old}}(s, a)\right]$
求1阶导数(梯度)时,$J(\pi_{old})$作为初始$\theta_{old}$的起点,相当于已经detach()了,无论几阶导数都是0。
所以$g = \nabla_{\theta} L_{\pi_{old}}(\pi(\theta)) = \nabla_{\theta} \mathbb{E}_{s, a \sim \tau \mid \pi_{old}} \left[ \frac{\pi(a \mid s, \theta)}{\pi_{old}(a \mid s) } A_{\pi_{old}}(s, a)\right] $
$=\mathbb{E}_{s, a \sim \tau \mid \pi_{old}} \left[ \frac{ \nabla_{\theta} \pi(a \mid s, \theta)}{\pi_{old}(a \mid s) } A_{\pi_{old}}(s, a)\right]$
对$J(\pi)$求导:
$\nabla_{\theta} J(\pi(\theta)) = \nabla_{\theta} \sum\limits_{s \sim \tau \mid \pi} \rho_{\pi_{\theta}}(s) \sum\limits_a \pi_{\theta}(a \mid s) A_{\pi_{old}}(s, a)$
product rule的两项,对$\rho_{\pi_{\theta}}(s)$求导的一项是$ \nabla_{\theta}\rho_{\pi_{\theta}}(s) \sum\limits_{a} \pi_{\theta}(a \mid s) A_{\pi_{old}}(s, a)$,里面$\sum\limits_a$的部分会变成0。所以只剩下product rule的另一项:
$\nabla_{\theta} J(\pi(\theta)) = \sum\limits_{s \sim \tau \mid \pi} \rho_{\pi_{\theta}}(s) \sum\limits_a \nabla_{\theta} \pi_{\theta}(a \mid s) A_{\pi_{old}}(s, a)$
当$\theta=\theta_{old}$时,
$\nabla_{\theta} J(\pi(\theta)) \mid _{\theta=\theta_{old}} = \sum\limits_{s \sim \tau \mid \pi} \rho_{\pi_{\theta}}(s) \sum\limits_a \pi_{\theta=\theta_{old}} \frac{\nabla_{\theta} \pi_{\theta}(a \mid s)} {\pi_{\theta=\theta_{old}}} A_{\pi_{old}}(s, a)$
$ = \mathbb{E}_{s, a \sim \tau \mid \pi_{old}} \left[ \frac{ \nabla_{\theta} \pi(a \mid s, \theta) \mid _{\theta=\theta_{old}}}{\pi_{old}(a \mid s) } A_{\pi_{old}}(s, a)\right]$
可以得到$\nabla_{\theta} J(\pi(\theta)) \mid _{\theta=\theta_{old}} = \nabla_{\theta} L_{\pi_{old}}(\pi(\theta)) \mid _{\theta=\theta_{old}}$
J与L在$\theta_{old}$处的梯度是一样的,又因为$M(\pi)=L_{\pi_{old}}(\pi)-CD_{KL}(\pi_{old} || \pi)$,那么在$\theta=\theta_{old}$处,$D_{KL}(\pi_{old} || \pi)$的一阶导是0,因为$D_{KL} \ge 0$,那么只要是连续的,在$\theta=\theta_{old}$时,$KL=0$且一阶导也必定是0。
另一方面对约束项求导时,max操作不方便处理,于是改成mean操作,约束项变成
$D = \frac{1}{T} \sum\limits_{t \sim \tau_{old}} D_{KL}\left[ \pi_{old}(\cdot \mid s_t) || \pi(\cdot \mid s_t) \right] \le \delta$
接下来只需要找到合适的lagrange multiplier $\beta$,优化$L – \beta D$就可以了。
根据trusted region边界的大小$\delta$,$\beta$会存在一个相应的最大值。
首先说一下如何在trusted region内进行优化:
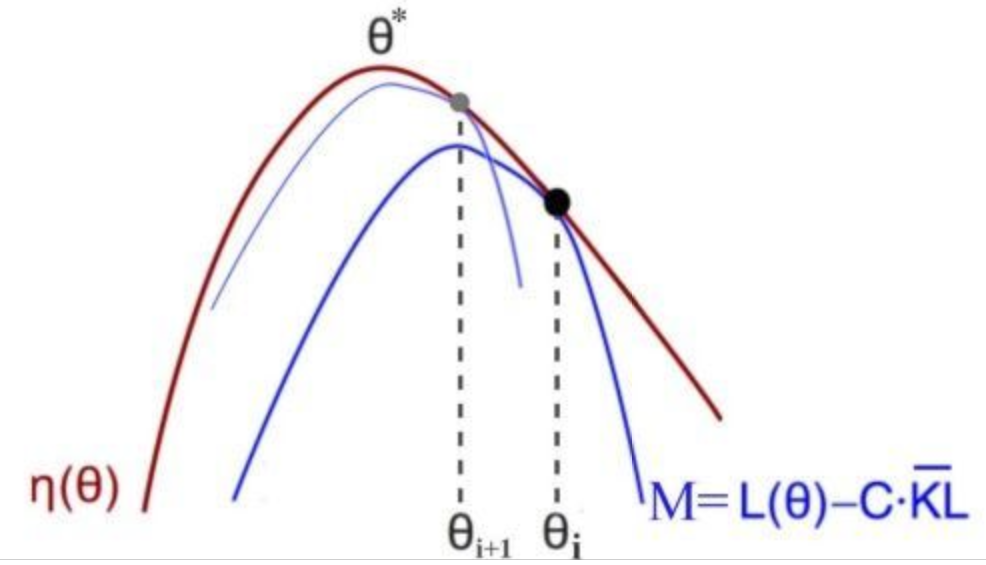
图中的$\eta$实际上就是$J$;i代表旧参数,i+1代表新参数。从前面的推导中,可以得出这几个结论:
- $M(\pi_{old})=J(\pi_{old})$
- $M$是$J$的下界
- L与J在$\theta_{old}$处一阶导一样,且由于KL的一阶导是0,导致M与J的局部一阶导也一样。
更新$\theta$的方法是这样的:计算当前M曲线的最优解,之后将下一步的$\theta$放在这里,更新参数后计算新M以及它的最优解。重复以上步骤即可。每一次计算$\theta$的更新方向并更新之前,起点$\theta_{old}$会被设置为当前的$\theta$,即先让$\theta_{old}=\theta_{cur}$,之后再计算$g \mid _{\theta=\theta_{old}}$ 与 $\nabla_{\theta}^{2} D \mid _{\theta=\theta_{old}}$
将$L$与$D$分别展开到至少一项与$\theta$相关的非0项,即
$L(\theta) \approx L(\theta_{old}) + g^T(\theta-\theta_{old})$
$D_{KL}^{mean} [\pi_{old} || \pi] \approx \frac{1}{2} (\theta-\theta_{old})^T \boldsymbol{H} (\theta-\theta_{old})$
优化目标就变成了:
$$\theta_{new} = \mathop{\arg \max}_{\theta} g^T(\theta-\theta_{old}) $$
subject to $\frac{1}{2} (\theta-\theta_{old})^T \boldsymbol{H} (\theta-\theta_{old}) \le \delta$
加上lagrange multiplier转化成无bound优化
$Gain = g^T(\theta-\theta_{old}) – \lambda \left( \frac{1}{2} (\theta-\theta_{old})^T \boldsymbol{H} (\theta-\theta_{old}) – \delta \right) $
让$\beta \boldsymbol{s} = \theta – \theta_{old}$
$0=\nabla_{\boldsymbol{s}} G = \boldsymbol{g} – \lambda \boldsymbol{H} \boldsymbol{s}$
$\boldsymbol{s}$的方向是$\boldsymbol{s}^* = \boldsymbol{H}^{-1} \boldsymbol{g}$,且要让$\lambda = 1$时,$s^*Hs^*=\delta$,$s^*$是M的最优解,那么需要的比例$\beta$就是$\beta = \sqrt{ \frac {2\delta} {\boldsymbol{s}^T \boldsymbol{H} \boldsymbol{s}}}$
优化方式则是沿着这个方向进行line search,首先从$M$的理论最优解$s^* = \boldsymbol{H}^{-1} \boldsymbol{g}$开始,如果loss不出问题,kl距离在允许范围内,且代理损失$M(\pi_{new}) \ge M(\pi_{old})$,则这次更新是有效的。否则需要回滚到$\theta_{old}$,然后尝试缩减步长,使用更小的步长,例如$\theta_{new}^{\text{next_try}} = \theta_{old} + 0.5 * \beta \boldsymbol{s}^*$,再尝试更新。
3. 数学技巧
前面基本上完成了对TRPO的理论讲解,但实现TRPO时还需要解决两个问题。一是计算KL的二阶导Hessian的开销非常大,因为它不是$\frac {\partial scalar} {\partial vector}$,而是一个矩阵:
$H_{ij} = \frac {\partial} {\partial \theta_j} \frac {\partial D_{KL}} {\partial \theta_i} $
不过我们并不需要单独计算出$\boldsymbol{H}$本身,而是都会让它后面跟一个向量,例如$\boldsymbol{x}$,所以只需要计算$\boldsymbol{y} = \boldsymbol{H} \boldsymbol{x}$即可。至于求inverse的操作,$\boldsymbol{H}^{-1} \boldsymbol{g}$,可以交给conjugate gradient来解决,也不需要直接算出$\boldsymbol{H}^{-1}$。
这样$y_k = \sum\limits_{j} H_{kj} x_j = \sum\limits_j \frac {\partial} {\partial \theta_j} \frac {\partial D_{KL}} {\partial \theta_k} x_j $
$ = \frac {\partial} {\partial \theta_k} \sum\limits_j \frac {\partial D_{KL}} {\partial \theta_j} x_j$
这样只需要先求KL的一阶导,与后接的向量$\boldsymbol{x}$进行点乘,再对参数$\boldsymbol{\theta}$求一次导就可以了。这个步骤就是fisher vector product。
除了fisher vector product中的求导部分,TRPO并不需要使用反向传播,所以可以在numpy里计算更新。另外注意对梯度求导时,pytorch默认梯度张量是no_grad的,所以无法求二阶导。要解决这个问题,需要在用autograd求1阶导时设置retain_graph=True,create_graph=True
关于conjugate gradient方法,参见这里。
