序言
所有机器学习的原理,本质上都是对同一段信息在不同空间内的转换、过滤、重新表征,最终解码出一段可读信息。为了让最终信息可读,我们需要给最终输出的每一个bit赋予意义。如果是监督学习,则需要定义一个度量来描述输出信息与真实信息的距离。
列举常见的传统机器学习,我们可以发现大多数监督学习都遵循着这一机制。
SVM使用内核机制重新定义了两个向量的内积,经过centering这样一个定义原点的操作之后,可以很快看出内核机制实际上重新定义了两个样本间的欧式距离。而任意两点间的欧式距离被改变,则意味着坐标系的转换,并且转换过后的新坐标系基本上不再是直角坐标系了,很可能是一个更高或是更低维度流型上的曲线坐标系。这时优化度量margin loss再在新坐标系上尝试分割出正负样本的support vector的最大间隔,找到线性超平面即可。
所有回归,包括线性回归、回归树,以及各种boosting tree,其坐标转换部分也非常明显,从N维输入到1维输出的转换(不管线性还是非线性),之后接一个优化度量(KL距离既交叉熵、最小二乘、triplet loss,etc.)
贝叶斯流派的最终优化目标:$logP(x)$,其本质还是减少$H(Y|\hat Y)$,即增加预测分布与目标分布的互信息。其特征空间的转换的方法,就比较五花八门了,这里不细分析。
何为信息:
以一个二值编码的10维向量为例,其排列组合个数2^10=1024,根据香农熵的定义(具体原理以及与概率描述的熵的关系可以参照之前的文章),一个10维binary向量的最大可承载信息量是$log(1024) = 10$。同样是10维,假如不是binary,而是任意连续变量,那么有两种方法可以用来估算连续变量的熵:分箱法以及基于knn的估算,后者本质上是一种不均匀的分箱法,所以就拿分箱法举例,假如同样是0-1区间被分成20个区间,那么该10维向量的最大可承载信息量就是$log(20^{10}) \approx 43.219$。一个分布X,如果满足10维随机均匀分布,那么其混乱度最大,能够达到最大可承载信息。实际上无论是任何分布,只要出现更粗粒度的离散化操作,其熵H(X)必然会不可逆地减少,出现信息损失。
\[\]
我们通常定义下的熵是微分熵,与香农熵的关系仅相差了一项与分箱间隔$\delta x$相关的一项。这项可以被当作常量,比如float数据类型的epsilon error,所以后面的熵统一以H代替,不指明是香农还是微分熵了。
$$H_{shannon}(X)=-\int\limits_x p(x) log (p(x)) dx – log(\delta x)=H_{differential}(X) – log(\delta x)$$
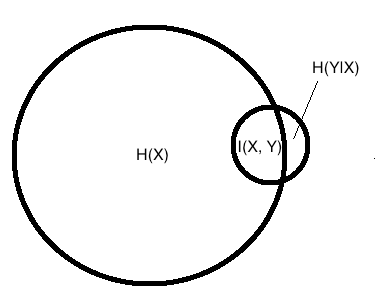
输入分布X内包含的所有信息,我们写作$H(X)$,然而我需要抽取的信号$H(\hat Y)$一般要小很多,这样才方便解读。我们的优化目标希望预测分布$\hat Y$与目标分布$Y$的距离(KL或Eucledian)越小越好。目标与输入的互信息$I(X,Y)$是有用的,而其他信息$H(X|Y)$以及$H(Y|X)$是无用的,因为要么信息与目标无关,要么我们无法解读它。
训练的最终目标是我们的$\hat{Y}$内包含的信息,从最初随机权重得到的绿色区域信息,逐渐遗忘掉X里与Y不相关的信息,同时尽量捕捉到X里与Y相关的信息。
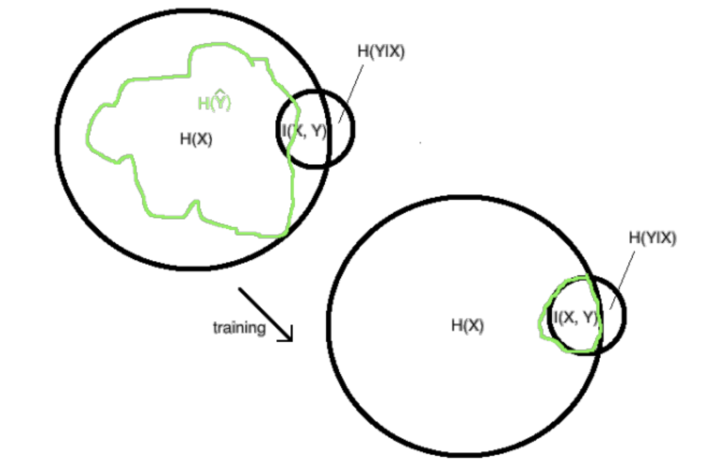
增加$I(\hat Y, Y)$的理由非常直观,因为监督学习时如果不学习目标Y的信息,自然无法预测出正确的结果。然而减少$I(X, \hat Y)$的理由就需要用范化误差来解释了。
$$R(\hat y)-R_{emp}(\hat y)\leq\sqrt{\frac{ln|H|+ln(2/\delta)}{2m}}$$
这里泛化误差上界 generalization error bound的推导,需要从霍夫丁不等式开始,具体细节就不展开了,感兴趣的可以网上搜推导过程。要以置信度$\delta$来确保样本分布emp与真实分布的预测值的差的绝对值不大于一个范化误差上界,有2种最有效方法:增加样本数量m或是减少$\hat y$的可取值的数量$|H|$。注意到信息量$H(\hat Y)$与$|H|$不相等,但是是有正相关性的。越有秩序的$\hat Y$,其可能的取值个数(分箱过后)$|H|$越小,且最大值不可能超过向量$\hat y$的信息承载上限。
\[\]
这样一来,只要减少$H(\hat Y)$,我们就能获得更优的范化误差表现,避免模型过拟合。不仅是在输出特征$\hat y$上需要进行压缩(尽量在保证$I(Y, \hat Y)$不减少的情况下),任何中间结果/隐藏层$h$的熵也可以压缩来改善过拟合。举个例子,当我需要判定一辆车是否能在机动车道行驶,我只需要知道车有4个轮子还是2个轮子就够了,不需要特征告诉我“有一辆蓝色4个轮子的车能够上机动车道”、“有一辆黑色4个轮子的车能够上机动车道”、“有一辆白色2个轮子的车不能上机动车道”……我不需要颜色这种不相关的信息,所以让特征层在进行特征变换时尽早遗忘掉颜色吧,这样还能节省一些训练需要的样本数。
信息瓶颈的实现方法:
通过上面的简单论证,得到了要想用有限的样本取得更小范化误差,同时让预测结果尽量接近真实目标,就需要最大化$I(\hat Y, Y)$同时减少$H(\hat Y)$或是$|H|$,那么接下来就分析一下哪些操作能够实现上面两个目标吧。
假设t=任意特征值,可以是输出层,也可以是任何一个传递信息的中间层。
$$d_{IB}=D_{KL}\left(p(y\mid x)\parallel p(y\mid t)\right)=\sum\limits _{y}p(y\mid x)log\frac{p(y\mid x)}{p(y\mid t)}$$
考虑上面KL距离的预期值
$E\left[d_{IB}\right]=\sum\limits _{x,t}p(x)p(t)d_{IB}(x,t)$
$=\sum\limits _{x,t,y}p(x)p(t)p(y\mid x)logp(y\mid x)-\sum\limits _{x,t,y}p(x)p(t)p(y|x)logp(y\mid t)$
使用$p(y\mid t)=\sum\limits _{x}p(y\mid x)p(x\mid t)$带入,得到
$=-\sum\limits _{x,t}p(x)p(t)H(Y\mid x)-\sum\limits _{t,y}\frac{p(x)p(t)}{p(x\mid t)}p(y\mid t)logp(y\mid t)$
$ =-\sum\limits _{x,{\color{red}t}}p(x){\color{red}{p(t)}}H(Y\mid x)+\sum\limits _{{\color{red}t}}\frac{{\color{red}{p(x)}}p(t)}{{\color{red}{p(x\mid t)}}}H(Y\mid t)$
$=-H(Y\mid X)+H(Y\mid T)=I(X;Y)-I(T;Y)$
X和Y的互信息取决于样本集,是个常量,所以训练过程中,逐渐减少
$D_{KL}\left(p(y\mid x)\parallel p(y\mid t)\right)=-H(Y|X) -\sum\limits_yp(y|x)log(p(y|t))$就可以增加$I(T, Y)$
再次忽略常量-H(Y|X),可以看到减少交叉熵,就是增加互信息I(T, Y)
学习的目标是由优化度量直接决定的,最小二乘的极小值也是类似的情况。
要压缩$H(T)$,可动用的手段就非常多了。一种方法是对信息的载体——向量,在其上面动手脚。
还有一种隐藏比较深但是更加常见的压缩方法,就是在梯度上增加噪音。梯度上的噪音会通过牛顿下降直接传到权重更新$\Delta w$上。
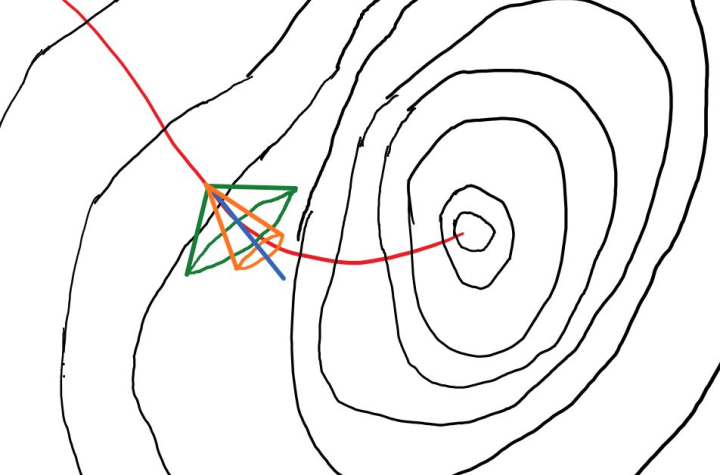
梯度下降时,完全无噪音的下降路径,应该在下降路径中时刻保持与真实分布X构成的等高线垂直,即上图中的红色路径。蓝色是红线在某一点的切线,也就是梯度下降无噪音信号。蓝线的方向是$\Delta \boldsymbol w = \eta \boldsymbol g_0 = \eta \nabla_{\boldsymbol w} \boldsymbol L(\boldsymbol w)$,
假如我们在蓝线的基础上加入垂直于$\boldsymbol g_0$的随机噪音,得到的有噪音梯度就可以看作是在一个圆锥的立体角范围内随机采样一个新的梯度$\boldsymbol g$。上图中绿色圆锥比橙色拥有更大噪音,橙色采样梯度则比绿色采样梯度拥有更大的信号噪音比。
添加的噪音,其作用不只是加快训练,更重要的是它也在帮助压缩向量t的信息H(T),可以减小范化误差。
为了简化说明问题,这里暂时把w和x都看作1维,高维情况的原理是一样的。$t=wx$,也暂时省去非线性部分relu,激活函数的确可以压缩H(T),但机制与离散化并没有本质差别,与梯度噪音是不同的。
