现有估算方法的局限性
交互信息以及熵的相关知识,请翻阅之前我写的博客。正常的做法是将连续数据离散分箱,之后用蒙特卡洛采样,统计每一个箱(bin)i,j 的概率$p(t_i)$和条件概率$p(t_i\mid x_j)$,再套用公式。 然而这种方法虽然理论上能在样本分布非常密集且均匀的情况下逼近精确的熵,需要的样本量与运算量却非常大,往往超过了一般实际场景所能搜集到的样本数,实际操作上基本不可取。
那么是否有方法能在有限的样本和不均匀的分布下,估算熵H(T)以及条件熵H(T|X)的方法呢?
答案是有,但是使用了一些假设,以及估算出熵的上限,而非熵本身。 论文参照了2篇:
https://arxiv.org/abs/1705.02436
https://arxiv.org/abs/1706.02419v1
建议与博客对照着看,毕竟论文里推导细节很少,啃起来还是有难度的,最终效果评估也请参照论文。
这里先澄清一下,论文中的熵实际上都是微分熵differential entropy $-\int\limits_tp(t)log(p(t))dt$,并非香农熵$-\sum\limits_{i}p_{i}log(p_{i})$。前者适用于连续变量,后者适用于离散变量。严格意义上的熵是指香农熵,两者之间不完全相等,具体见这篇文章。
以前博客里的所有提到的熵,都是香农熵,这篇文章里并没有注明是哪种熵,所以需要根据变量是离散还是连续性质,来判定熵与条件熵究竟是微分熵还是香农熵,并且在得到最终公式之前作出对应转换,才能计算出正确的交互信息。
论文中提供的代码都没有对两种熵的计算进行区分,公式里也忽略了这一点,但是在实际使用中,两种熵的差异还是会有很大影响的。
一系列合理假设
神经网络的任意一层的vector变量T(也包括输入层X)的分布p(t),都可以看作是一个高斯混合模型。
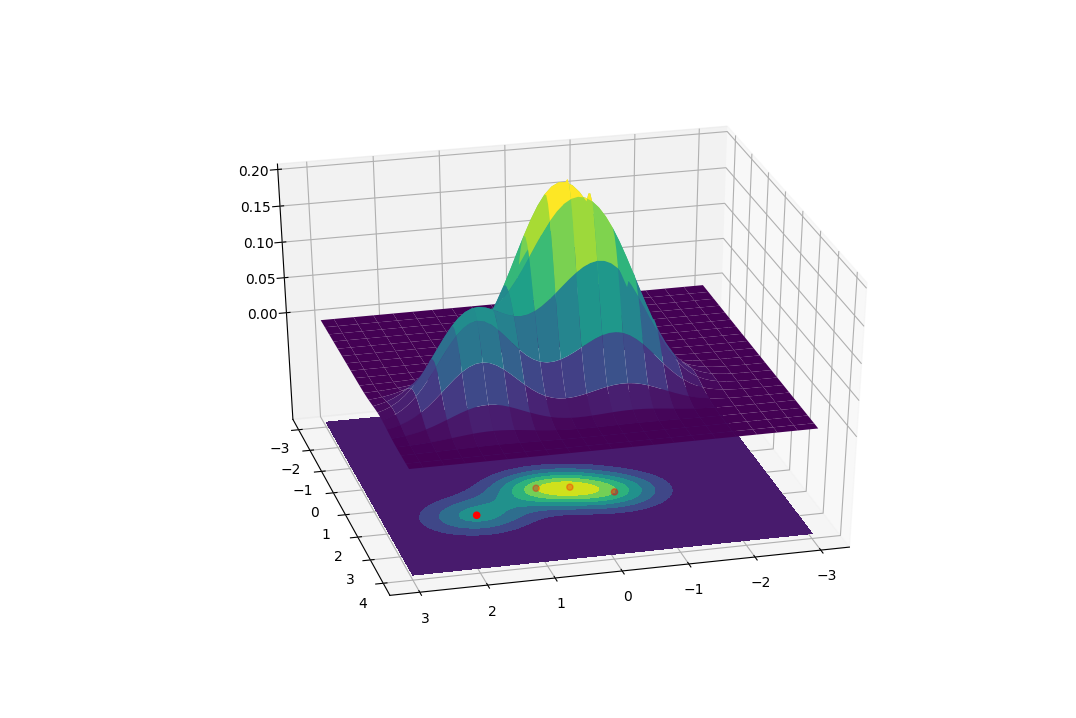
如图展示了一个4个样本组成的高斯混合模型:
$p(t)=\sum_{i}c_i Norm(\boldsymbol \mu_i , \boldsymbol t, \boldsymbol \sigma)$
每个样本的gaussian component分布都有同样的协方差矩阵$\boldsymbol {\sigma}=\begin{pmatrix}s^2 & 0\\ 0 & s^2 \end{pmatrix}$
$\boldsymbol \mu_i$是样本i在该层的预期值$\mathbb{E}[f(\boldsymbol x_i)]$,f是当前层的影射函数满足$\boldsymbol t=f(\boldsymbol x)$,输入层的映射函数可以看作Identity映射f(x)=x
$c_i=1/N$,N是样本总数。
图像只能展示二维希尔伯特空间$d=2$,对于任意高维的T与X,自行脑补即可,反正数学都是一样的。
这里有2个假设:
每个样本对最终分布的贡献方式相同,没有一个样本是特殊的。
样本贡献在各个维度方向上也是相同的,没有一个维度是特殊的。
让有限的样本混合出最准确的真实分布
使用高斯混合模型时,引入了一个超参$\boldsymbol \sigma$。当我们需要模拟出真实分布$p(t)$在某一个样本i所在的位置$p(t=t_i)$时,理所当然是样本i贡献了最多的p(t),其他N-1个样本贡献都不如这个样本高。当$s^2$变大时,每个样本的高斯分量$Norm(\boldsymbol \mu_i,\boldsymbol t, \boldsymbol \sigma)$都变得扁平一些,效果就是削弱了样本i在$t_i$位置的贡献,增强了其他N-1个样本在该位置的贡献。
我们希望任何单一样本的存在与否,对真实分布的影响都尽量小,因为只要是从T随机采样得到的样本集{t1, t2……tN},它背后的真实分布都应该都是一样的p(t)。这样才能保证在采样数不足的情况下,p(t)不会在缺乏采样的位置上变形太多,因为有其他样本的贡献来支撑这里的概率。
所以我们要在满足最大似然$\int log(p(t))dt$的同时,最大化$s$。
所以得到:
$p(i \mid j) = [(2 \pi)^d det(\boldsymbol \sigma)]^{-1/2}exp \{- \frac {\| \boldsymbol \mu_i – \boldsymbol \mu_j \|^2} {2s^2}\} = [(2\pi )^ds^{2d}]^{-1/2}exp\{ – \frac {\| \boldsymbol \mu_i – \boldsymbol \mu_j \|^2} {2s^2}\}$
除去样本i,剩余N-1个样本在$t_i$位置的贡献是:
$p(\neg i)=\frac 1 {N-1}\sum\limits_{i\neq j}p(i \mid j)$
论文中定义的leave-one-out log likelihood,就是按照这个思路,将所有样本点的贡献都排除一次,类似于cross validation的思路,求出任何情况下无论t的值是多少,单个样本的存在与否对整体样本集高斯混合出的分布p(t)的影响最小。
求出超参s在最大化log likelihood时的stationary point:
$\eta=\underset{s}{\arg\max}\sum\limits_ilog(p(\neg i))$
可解得当前网络参数$\boldsymbol \theta $得到的映射$\boldsymbol \mu =f_{\boldsymbol \theta} (\boldsymbol x)$下,通过计算不同样本两两高斯距离的到的最优gaussian component的协方差矩阵$\boldsymbol \sigma = \eta^2 \boldsymbol I$
where
$\eta(\boldsymbol \theta)=\underset{s}{\arg\max}\sum\limits_ilog \left( \frac 1 {N-1}\sum\limits_{i\neq j}[(2\pi )^ds^{2d}]^{-1/2}exp\left( – \frac {\|f_{\boldsymbol\theta} (\boldsymbol x_i) – f_{\boldsymbol \theta} (\boldsymbol x_j) \|^2} {2s^2}\right) \right)$
估算高斯混合的熵
前面对高斯混合模型的定义$p(\boldsymbol t)=\sum_{i}c_i Norm(\boldsymbol \mu_i, \boldsymbol t, \boldsymbol \sigma)$中,将第i个样本的高斯分量简写为$p_i(\boldsymbol t)=Norm(\boldsymbol \mu_i, \boldsymbol t, \boldsymbol \sigma)$
将高斯混合的过程分作2步来看:首先从一个均匀分布C中以概率$c_i=1/N$选择一个i,之后以第i个样本的映射值预期$\boldsymbol \mu_i$为中心,放置高斯分量$p_i(\boldsymbol t)$
两个相互独立的事件的概率积联,得到联合概率
$p_{T,C}(\boldsymbol t, i)=p_i(\boldsymbol t)c_i$
推算出
$H(T|C)=\sum\limits_ic_iH(T \mid c_i)$
且$H(T\mid c_i)=-\int\limits_tp(\boldsymbol t \mid c_i)log(p(\boldsymbol t \mid c_i))$
$=-\int\limits_t \frac {p_{T,C}(\boldsymbol t, i)} {c_i}log \left( \frac {p_{T,C}(\boldsymbol t,i)} {c_i} \right)$
$=H(p_i(\boldsymbol t))$
所以$H(T\mid C)=\sum\limits_i c_iH(p_i)$
推算高斯混合的熵:
$H(T)=-\int\limits_{t} \sum \limits_{i} c_ip_i(t)log(\sum\limits_jc_jp_j(t))dt$
$=-\sum\limits_i c_i\mathbb{E}_{p_i}\left[ log(\sum\limits_jc_jp_j(t))\right]$
使用Jensen inequality
$\leqslant -\sum\limits_i c_i log \sum\limits_j c_j \mathbb{E}_{p_i}\left[ p_j(t) \right]$
将$p_j(t)$写成$exp\{log(p_j(t))\}$之后再次使用Jensen inequality
$\leqslant -\sum\limits_i c_i log \sum\limits_j c_j exp\{ \mathbb{E}_{p_i}\left[ log(p_j(t)) \right]\}$
$=-\sum\limits_i c_i log \sum\limits_j c_j exp\{ \int\limits_{\boldsymbol t=-\infty}^{\infty}p_i(t)log(p_j(t))dt\}$
注意到KL距离的定义$D_{KL}(p_i \| p_j)=\int p_i(t)log \left( \frac {p_i(t)} {p_j(t)} \right) dt=-H(p_i)-\int p_i(x)log(p_j(x)) dt$
代入得到
$H(T) \leqslant -\sum\limits_i c_i log \sum\limits_j c_j exp\{ -H(p_i)- D_{KL}(p_i \| p_j)\}$
$=-\sum\limits_i c_i log \sum\limits_j c_jexp\{-H(p_i)\} – \sum\limits_{i} c_i log \sum\limits_j c_jexp\{-D_{KL}(p_i \| p_j)\}$
$=\sum\limits_i c_iH(p_i) – \sum\limits_{i} c_i log \sum\limits_j c_jexp\{-D_{KL}(p_i \| p_j)\}$
第一项前面推导过正好是H(X|C)
同时注意到第二项存在上限(因为kl距离总>=0,导致c_j乘上一个小于等于1的数字,取log时负数更大)
$- \sum\limits_{i} c_i log \sum\limits_j c_jexp\{-D_{KL}(p_i \| p_j)\} \leqslant – \sum\limits_{i} c_i log \sum\limits_j c_j=H(C)$
得到一个熵的estimator $\hat{H}(T)$,满足下列区间:
$H(T) \leqslant \hat{H}(T) = H(T \mid C)- \sum\limits_{i} c_i log \sum\limits_j c_jexp\{-D_{KL}(p_i \| p_j)\} \leqslant H(T \mid C) + H(C)=H(T, C)$
值得注意的是,$\hat{H}(T)$可以在有限样本集内被评估出来,具体细节后面会说。论文中该估值的效果还算可以,尤其是维度比较多的时候。不管怎样比起只能蒙特卡洛采样估计的H(T),在所需样本数以及计算量上已经占据了非常大的优势了。
从熵估值到交互信息:
神经网络中隐藏层分布T与输入层分布X满足
$I(X,T)=H(T)-H(T|X)$
因为T满足高斯混合模型,代入上文的estimator
$\leqslant \sum\limits_ic_iH(p_i)-\sum\limits_{i} c_i log \sum\limits_j c_jexp\{-D_{KL}(p_i \| p_j)\} – H(T\mid X)$
定义X层的概率密度分布是q(x),T层的概率密度分布是p(t)
$H(T\mid X)=\int\limits_xq(x)H(T\mid x) dx$
$=-\int\limits_xq(x)\int\limits_tp(t\mid x)log(p(t \mid x))dtdx$
假设真实情况中引入了一些噪音,即使输入相同,输出也有一些不确定性$\boldsymbol \xi=\begin{bmatrix}
\zeta^2 & 0 & \cdots\ &0\\
0 & \zeta^2 & \cdots\ & 0\\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots\ & \zeta^2\\
\end{bmatrix}$,且不确定性呈高斯分布:$p(t\mid x)=Norm(f_\theta(\boldsymbol x),\boldsymbol t, \boldsymbol \xi)$
正态分布的熵积分得到
$H(T\mid \boldsymbol x)=-\int\limits_t Norm(f_\theta(\boldsymbol x),\boldsymbol t, \boldsymbol \xi) log \left( Norm(f_\theta(\boldsymbol x),\boldsymbol t, \boldsymbol \xi)\right) dt$
$=\frac 1 2log\left[(2\pi e)^ddet(\boldsymbol \xi)\right]$
具体推导过程就省略了,网上能查。d是向量t的维度数。
因为这玩意不依赖于x,所以拎出对x的积分,剩下$\int\limits_x q(x) dx = 1$
所以$H(T\mid X)=\frac 1 2log\left[(2\pi e)^ddet(\boldsymbol \xi)\right]=\frac 1 2log\left[(2\pi e)^d\zeta^{2d}\right]$
同理对于任意样本的高斯分量
$H(p_i)=\frac 1 2log\left[(2\pi e)^ddet(\boldsymbol \sigma)\right]$
其中我们前面也已经求出了高斯分量协方差的最优解$\boldsymbol \sigma=\eta^2\boldsymbol I$
然而之前求解$\eta$的时候并没有考虑真实样本的噪音,实际情况当噪音存在时,$\boldsymbol \sigma=(\eta^2 + \zeta^2) \boldsymbol I$,既variance + noise。noise的来源可以是SGD,或是权重更新$\theta$时的梯度。
所以$H(p_i)=\frac 1 2log\left[(2\pi e)^d(\eta^2+\zeta^2)^d\right]$
还剩KL距离一项没分析的:
$D_{KL}(p_i(t)\|p_j(t))=\int\limits_tp_i(t)log(p_i(t))dt – \int\limits_tp_i(t)logp_j(t)dt$
把$p_j(\boldsymbol t)$写成完整正态分布形式$\left[ (2\pi )^d det(\boldsymbol \sigma)\right]^{-1/2}exp\{-\frac 1 2 (\boldsymbol \mu_j – \boldsymbol t)^T\boldsymbol \sigma ^{-1} (\boldsymbol \mu_j – \boldsymbol t)\}$之后代入上式
$=-\frac 1 2log\left[(2\pi e)^ddet(\boldsymbol \sigma)\right] – log\left[ (2\pi )^d det(\boldsymbol \sigma)\right]^{-1/2} – \int\limits_t p_i(t)log \left(exp\{-\frac 1 2 (\boldsymbol \mu_j – \boldsymbol t)^T\boldsymbol \sigma ^{-1} (\boldsymbol \mu_j – \boldsymbol t)\} \right)dt$
这里凑巧i与j的高斯分量都在T层,所以两个协方差相同,不过还是给$\boldsymbol \sigma$个下标区分一下,方便与标准形式对照
$=-\frac 1 2log\left[(2\pi e)^ddet(\boldsymbol \sigma_i)\right] – log\left[ (2\pi )^d det(\boldsymbol \sigma_j)\right]^{-1/2} – \mathbb{E}_{p_i}\left[-\frac 1 2 (\boldsymbol \mu_j – \boldsymbol t)^T\boldsymbol \sigma_j ^{-1} (\boldsymbol \mu_j – \boldsymbol t) \right]$
$=-\frac d 2 + \frac 1 2 log\left( \frac {det(\boldsymbol \sigma_j)} {det(\boldsymbol \sigma_i)} \right) – \mathbb{E}_{p_i}\left[-\frac 1 2 (\boldsymbol \mu_j – \boldsymbol t)^T\boldsymbol \sigma_j ^{-1} (\boldsymbol \mu_j – \boldsymbol t) \right]$
inverse一个diagonal matrix 得到$\boldsymbol \sigma_j ^{-1}= 1/(\eta_j^2 + \zeta^2)\boldsymbol I$
同时$\mathbb{E}_{p_i}\left[ \boldsymbol k^T \boldsymbol k \right]= d(\eta_i^2 + \zeta^2)+ \| \mathbb{E}_{p_i}\left[ \boldsymbol k \right]\|^2$对于任意向量k
所以
$\mathbb{E}_{p_i}\left[(\boldsymbol \mu_j – \boldsymbol t)^T\boldsymbol \sigma_j ^{-1} (\boldsymbol \mu_j – \boldsymbol t) \right]= \frac 1 {\eta_j^2+\zeta^2} \left( \|\boldsymbol \mu_j \|^2 – \boldsymbol \mu_j^T\boldsymbol \mu_i – \boldsymbol \mu_i^T \boldsymbol \mu_j + \|\boldsymbol \mu_i \|^2 + d(\eta_i^2 + \zeta^2) \right)$
$=(\boldsymbol \mu_j – \boldsymbol \mu_i)^T\boldsymbol \sigma_j^{-1}(\boldsymbol \mu_j – \boldsymbol \mu_i) + d \frac {\eta_i^2 + \zeta^2} {\eta_j^2 + \zeta^2}$
$=(\boldsymbol \mu_j – \boldsymbol \mu_i)^T\boldsymbol \sigma_j^{-1}(\boldsymbol \mu_j – \boldsymbol \mu_i) + tr(\boldsymbol\sigma_j^{-1}\boldsymbol\sigma_i)$
两个gaussian分布的KL距离的标准形式:
$D_{KL}(p_i(t)\|p_j(t))=\frac 1 2 \left[ – d + log\left( \frac {det(\boldsymbol \sigma_j)} {det(\boldsymbol \sigma_i)} \right) + (\boldsymbol \mu_j – \boldsymbol \mu_i)^T\boldsymbol \sigma_j^{-1}(\boldsymbol \mu_j – \boldsymbol \mu_i) + tr(\boldsymbol\sigma_j^{-1}\boldsymbol\sigma_i) \right]$
这个问题里$\eta_i=\eta_j$所以也可以化简成:
$D_{KL}(p_i(t)\|p_j(t))=- \frac d 2 + \frac {\| \boldsymbol\mu_j – \boldsymbol \mu_i \|^2} {2(\eta^2+\zeta^2)} + \frac d 2=\frac {\| \boldsymbol\mu_j – \boldsymbol \mu_i \|^2} {2(\eta^2+\zeta^2)}$
现在把交互信息的所有项拼起来:
$I(X,T)\leqslant \sum\limits_ic_iH(p_i)-\sum\limits_{i} c_i log \sum\limits_j c_jexp\{-D_{KL}(p_i \| p_j)\} – H(T\mid X)$
$=\frac 1 2log\left[(2\pi e)^d(\eta^2+\zeta^2)^d\right] – \frac 1 2log\left[(2\pi e)^d\zeta^{2d}\right] – \sum\limits_i c_ilog\sum\limits_jc_j exp\{ – \frac {\| \boldsymbol\mu_j – \boldsymbol \mu_i \|^2} {2(\eta^2+\zeta^2)}\}$
$= – \frac d 2 log \left( \frac {\zeta^2} {\eta^2 + \zeta^2} \right) – \frac 1 N\sum\limits_i log\left( \frac 1 N \sum\limits_jexp\{ – \frac {\| \boldsymbol\ f_\theta(\boldsymbol x_j) – f_\theta(\boldsymbol x_i) \|^2} {2(\eta^2+\zeta^2)} \} \right)$
这里第一项比论文中多乘了一个1/2,不知道是论文出错还是自己算错,应该影响不是很大。
如何在样本集上计算I(T, X)
论文中将$\zeta$看作是$\theta$的一部分,都需要被学习优化。所以在解$\eta$的时候,把$s^2$拆成2部分:变量$s’^2$与常量$\zeta^2$,求极值时针对前者求导。
$\zeta$的初始化不同于$\theta$,论文中建议从比较小的$\zeta$初始,这样一开始可以获得比较准确的更新梯度。
1. 从给定的样本集D中,拆出2个子集A和B,B数量较多,理论上没有说不能出现重叠,反正论文提供的项目代码里A是从训练集中轮循size=128的minibatch,B是从训练集中完全随机采样的1000个样本。
2. 用B子集的样本来计算$\eta$:
固定网络权重$\theta$以及noise $\zeta$,之后对s’求极值:
$\eta(\boldsymbol \theta)=\underset{s’}{\arg\max}\sum\limits_ilog \left( \frac 1 {N-1}\sum\limits_{i\neq j}[(2\pi )^d(s’^2+\zeta^2)^{d}]^{-1/2}exp\left( – \frac {\|f_{\boldsymbol\theta} (\boldsymbol x_i) – f_{\boldsymbol \theta} (\boldsymbol x_j) \|^2} {2(s’^2+\zeta^2)}\right) \right)$
上面的式子对s’连续可微分,所以使用梯度下降方法计算即可得到混合高斯的variance $\eta$。
3. 假设A集中每个样本的高斯分量也有相同的variance以及noise,在A中选取一个样本i,计算$f_\theta(x_i^{(A)})$作为$\boldsymbol \mu_i$,之后从$Norm(\boldsymbol \mu_i, \boldsymbol t, \boldsymbol \xi)$中采样获得$\boldsymbol t_i^{(A)}$,即样本集A中第i个样本在当前隐藏层分布T中的一个采样值$\boldsymbol t$
4. 在B集上按照estimator:$I(X,T) \approx – \frac d 2 log \left( \frac {\zeta^2} {\eta^2 + \zeta^2} \right) – \frac 1 N\sum\limits_i log\left( \frac 1 N \sum\limits_jexp\{ – \frac {\| \boldsymbol\ f_\theta(\boldsymbol x_j) – f_\theta(\boldsymbol x_i) \|^2} {2(\eta^2+\zeta^2)} \} \right)$估算当前iteration的交互信息
5. $\boldsymbol t_i^{(A)}$被作为后面decoder部分的输入,参与计算loss(常规NN的交叉熵or最小二乘之类的),之后SGD更新$\theta$以及$\zeta$,进入下个iteration
6. 循环2-4,完成一个普通训练过程中针对交互信息I(T,X)的监控。
使用限制主要是T和X都要是连续变量,且可以看作高斯混合模型。
估算I(Y,T),Y是离散分类
$I(T, Y)=H(Y) – H(Y \mid T)$
改写第二项,估算一个它的上限:
$H(Y \mid T)=-\int\limits_t p(t)\sum\limits_kp(k \mid t)log(p(k\mid t)) dt $
$\leqslant H(P(Y\mid T)) + D_{KL}(P(Y\mid T) \| Q(Y \mid T))$
$= -\int\limits_t p(t)\sum\limits_kp(k \mid t)\left[ log(p(k\mid t)) – log \left( \frac {p(k \mid t)} {q(k \mid t)} \right) \right] dt $
$= -\int\limits_t p(t)\sum\limits_kp(k \mid t)\left[ log( {q(k \mid t)}) \right] dt $
=$\mathbb{C}(P(Y \mid T) \| Q(Y \mid T))$
即真实分布P(Y | T)与任意分布Q(Y | T)的交叉熵的预期值
所以I(T, Y)的下限也就出来了:
$I(T, Y) \geqslant H(P(Y)) – \mathbb{C}(P(Y \mid T) \| Q(Y \mid T))$
我们希望分布Q(Y|T)尽量接近P(Y|T),这样交叉熵趋向于熵,上式的不等号也就趋近于等号了。
所以我们需要一个训练到收敛的网络,然后估算真实分布(target)与拟合分布(predict)的交叉熵的预期值。
$\mathbb{C}(P(Y \mid T) \| Q(Y \mid T))=\frac 1 N \sum\limits_{i=1}^N \sum\limits_k \delta(y_{i}^{(target)}=k)log(q(y^{(predict)}(f_\theta(\boldsymbol t_i))=k))$
实际上就是样本集内target与softmax出来的logits的cross entropy loss的平均值
我们在训练网络时不断最小化这玩意,实际目的就是在尽量增加I(T, Y),因为H(Y)就是个常量而且很好估算。
论文里使用的$\boldsymbol t_i$并非直接从样本集中抽取,而是在估算I(T, X)流程第三步中在A子集样本加入高斯噪音后采样得到的$\boldsymbol t_i^{(A)}$,理论上是比$\boldsymbol t_i$更符合高斯混合分布的,噪音的引入也增加了H(T),所以能帮助在训练NN时使I(Y,T)增大,但是对于估算I(T, Y)的实际效果比不加噪音怎样,也不清楚。
Information Bottleneck方法:
论文里将优化问题写成了:
$L=I(X, T) – \lambda I(Y, T)$的拉格朗日乘子形式,即满足I(Y,T)=H(Y)的条件同时,最小化I(X, T)
所以只需要找出I(X,T)的上限以及I(Y,T)的下限,即可获得L的上限,之后通过手动调整$\lambda$与梯度下降,求出最小的L上限,即可同时让I(X,T)与I(Y,T)的估值各自收敛到它们的真实值上。
最终挑战:I(Y, X)的上限?
其实我个人最关注的是这个,直接决定了数据质量是否可用。
$I(X, Y) = H(X) – H(X \mid Y)$
要求LHS的上限,需要$H(X)$的上限与$H(X \mid Y)$的下限
$H(X)$上限的估算之前已经推导过了,只需要把T换成X即可,最方便的一点是这时候不需要训练网络来获取$f_{\theta}(·)$了。
y从Y中采样,有k={1, 2, …… K}种分类
$H(X \mid Y)=\sum\limits_kp_kH(X \mid k)$
其中$p_k$好统计,给定k之后,从子集$D_k = \{(x_i, y_i)\forall y_i=k\}$中计算$H(X^{(D_k)})$的下限,即可得到$H(X \mid k)$
所以问题转化为求出H(X)的下限了。
论文中给出的下限是:
$H(X) \geqslant H(X \mid C) – \sum\limits_i c_i \sum\limits_j c_jexp\{- D_B(p_i \| p_j)\}$
其中$D_B(\cdot \|\cdot·)$是Bhattacharyya distance,定义为:
$D_B(p_i(t) \| p_j(t))=-log\int\limits_t \sqrt{p_i(t)p_j(t)} dt$
具体推到过程论文里有写,我这也不复述了。
从数据集样本中拟合高斯分量的方法与之前估算H(X)上限时一样,找到协方差矩阵元素$\eta$之后,写出对角线协方差$\boldsymbol \sigma$
维基百科里查找到两个高斯分布的Bhattacharyya距离是:
$D_B(p_i \| p_j)= \frac 1 8 (\boldsymbol \mu_j – \boldsymbol \mu_i) \bar{\boldsymbol \sigma}^{-1} (\boldsymbol \mu_j – \boldsymbol \mu_i) + \frac 1 2 log \left( \frac {det(\bar{\boldsymbol \sigma})} {\sqrt{det(\boldsymbol \sigma_i) det(\boldsymbol \sigma_j)}} \right)$
其中$\bar{\boldsymbol \sigma} = \frac {\boldsymbol \sigma_i + \boldsymbol \sigma_j} 2 $
具体推导细节也暂时省略了,当然这里$\boldsymbol \sigma_i$与$\boldsymbol \sigma_j$也是相等的。
综上所述:
上限
$H(X) \leqslant -\sum\limits_i c_i log \sum\limits_j c_jexp\{-H(p_i)\} – \sum\limits_{i} c_i log \sum\limits_j c_jexp\{-D_{KL}(p_i \| p_j)\}$
$=\sum\limits_i c_iH(p_i) – \sum\limits_{i} c_i log \sum\limits_j c_jexp\{-\frac {\| \boldsymbol\mu_j – \boldsymbol \mu_i \|^2} {2\eta^2}\}$
下限
$H(X) \geqslant -\sum\limits_i c_i log \sum\limits_j c_jexp\{-H(p_i)\} – \sum\limits_{i} c_i log \sum\limits_j c_jexp\{-D_{B}(p_i \| p_j)\}$
$=\sum\limits_i c_iH(p_i) – \sum\limits_{i} c_i log \sum\limits_j c_jexp\{-\frac {\| \boldsymbol\mu_j – \boldsymbol \mu_i \|^2} {8\eta^2}\}$
如此一来I(X,Y)的上限就能够在有限样本集内被估算出来了,可以在训练模型之前就先对数据质量进行一下分析。其背后依赖的假设是样本集输入数据x的分布X,可以被混合高斯模型模拟。
