无噪音下降路径
考虑一个通用的机器学习场景:
客观存在一个分布$p(\boldsymbol{x},y)$,定义为预测集predict set的样本分布,也叫做真实样本分布,理论上存在近乎无穷多个样本。
然后从真实分布中,采样得到一个比较大的训练样本集,样本数量N足够大以至于分布$p_{tr}(\boldsymbol{x},y) \approx p(\boldsymbol{x},y)$接近真实分布
假设我们设计好了一个神经网络,那么损失函数$l$在当前真实分布下的预期值$L(\boldsymbol {w})={\mathbb E}_{p(\boldsymbol{x},y)}l(\boldsymbol{w},\boldsymbol{x},y)$理论上是存在的,且可以从训练集中近似得到$L(\boldsymbol{w}) \approx \frac {1} {N} \sum\limits_{i=1}^{N}l(\boldsymbol{w}, \boldsymbol{x}_i, y_i)=L_{emp}(\boldsymbol {w})$
我们把$L_{emp}叫做经验风险$,$L(\boldsymbol {w})$叫做期望风险。暂时二者先被认为是相等的。
一旦损失函数的函数被确定,就可以画出一个等高线图,高度(垂直纸面轴)代表loss,横轴竖轴变量分别是$\boldsymbol{w}$的两个维度

注意这里的等高线是真实分布的损失函数预期,而非训练集sum出的损失函数预期,两者会有微小差异,不过可以先忽略。
我们随机选取一点作为起点,在任何时刻都保持与等高线垂直的方向前进,即任意时刻都沿当前位置梯度反方向前进,即可得到最快下降线。
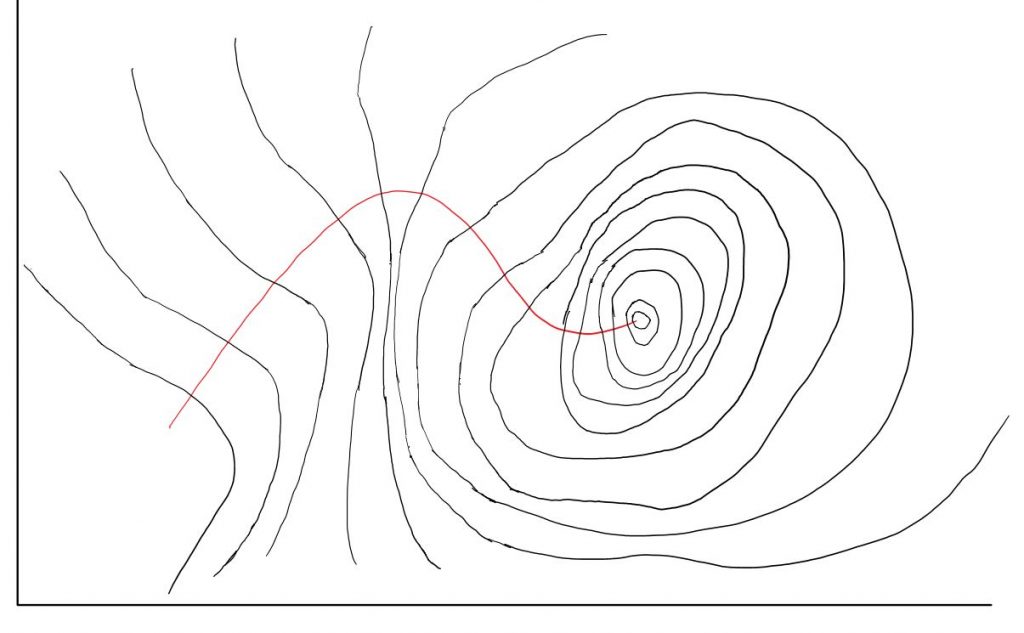
红线被定义为无噪音梯度下降路径
mini batch下的某一轮梯度下降
从训练集中切分mini batch,batch大小=k,$1 \le k \le N$,即一个mini batch内包含k个样本。当k=1时训练过程是sgd,当k=N时训练过程变成bgd。
bgd的等高线形状因为非常接近真实等高线,所以可以认为梯度$\boldsymbol {g}_{bgd} = \nabla L_{bgd}=\nabla L$,在等高线图上任意一点,$\boldsymbol{g}_{bgd}$都等于无噪音梯度下降路径的切线。
在sgd的情况下$L_{sgd}=l(\boldsymbol{w}, \boldsymbol{x}, y) \neq L$,所以很明显等高线形状会完全不同于BGD以及无噪音,计算出的梯度$\boldsymbol {g}_{sgd}$也会明显不同。
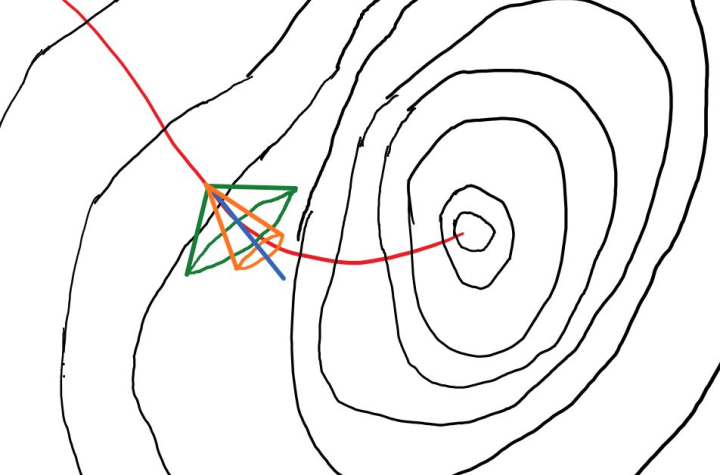
蓝色是$\boldsymbol {g}_{bgd}$,也是无噪音路径的切线的方向,因为bgd对应的mini batch在训练集中只能分割出一个,所以蓝线只有一条,bgd的噪音可以看作大约是0。$\zeta_{bgd}(\boldsymbol{w}) = 0$
绿色圆锥体是$\boldsymbol {g}_{sgd}$出现的范围的一个大致轮廓,一轮更新算出的梯度,有大概率落在绿色圆锥范围内。
因为sgd的mini batch可以从训练集中分割出N个,每个batch都能计算出一个sgd梯度,这N个梯度与无噪音梯度的差,构成一个集合{($\boldsymbol {g}_{sgd}(\boldsymbol{w}) – \nabla_{w} L(\boldsymbol{w}))$},这个集合的variance,是sgd带来的噪音。$\zeta_{sgd}(\boldsymbol{w})=var(\{(\boldsymbol {g}_{sgd}(\boldsymbol{w}) – \nabla_w L(\boldsymbol{w}))\})$
当k取1到N中间的一个整数时,可以分割出 $N / k$个mini batch,之后类似sgd的噪音定义,我们得到mini batch的噪音$\zeta_{mini}$同时用橙色圆锥来代表mini batch梯度大概率出现的范围。
注意到从sgd到bgd,噪音是逐渐减小的。如果我们把信号定义为最速下降线的切线,那么信噪比就是在逐渐增大。
**高信噪比明确指引梯度更新往正确的方向前进,低信噪比则会让前进方向呈现更多不确定性。**
随着mini batch分布下的$L_{mini}(\boldsymbol {w})=\sum\limits_{i \in mb} l(\boldsymbol {w}, \boldsymbol {x}_i, t_i)$越来越靠近真实$L(\boldsymbol {w}) = \int\limits_{\boldsymbol {x}, t} p(\boldsymbol {x}, t) l(\boldsymbol {w}, \boldsymbol {x}, t) d\boldsymbol{x}dt$,batch大小k增加,噪音$\zeta_{mini}(\boldsymbol{w})$逐渐减小,圆锥范围逐渐收紧直到变成一条直线。
整个梯度下降路径中的噪音
上面定义了在loss等高线图上任意一点使用不同batch大小进行梯度下降的噪音,然而整个路径的噪音,需要对点噪音沿路径积分:
$\xi_{mini}=\frac {1} {S}\int\limits_{s}\zeta_{mini}(\boldsymbol{w})ds$,S是路径的长度$S=\int\limits_{s}ds$,s是下降路径上已经“行驶”过的距离变量。
首先看一下sgd的一条下降路径,因为噪音的存在,不会在每一轮都沿着最速下降线的方向,走过的路程也是不规则的,但是总体趋势还是朝着最优解方向前进的。
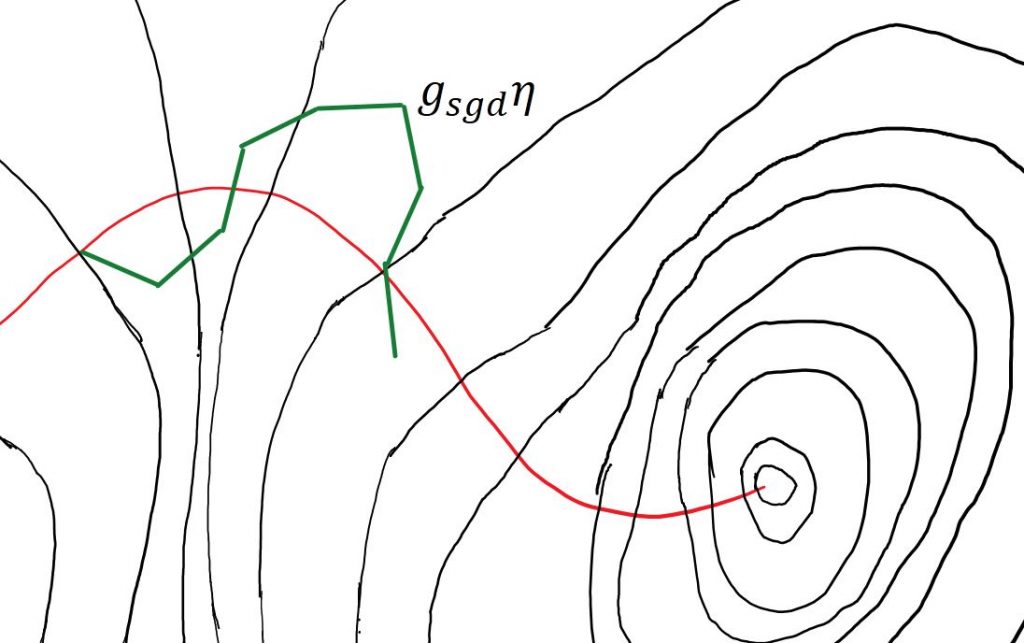
注意到这段路径是由若干段直线拼接而成,每一段直线的长度是sgd梯度与学习速率$\eta$的乘积。
对红色最速下降线路径GDPath上的噪音积分,可得$\xi= \frac {1} {S}\int\limits_{s \in GDPath}\zeta(\boldsymbol {w})ds=0$,因为$\zeta(\boldsymbol{w})$在该路径任何位置上都是0
对绿色sgd路径上的噪音积分,可得到$\xi_{sgd} > 0$
接下来看BGD的路径,需要在每一段线段的起点保证bgd梯度的方向垂直于起点位置的等高线,然后沿着该方向前进$g_{bgd}\eta$长度的直线距离,之后标记线段终点同时也是下一轮迭代的起点。
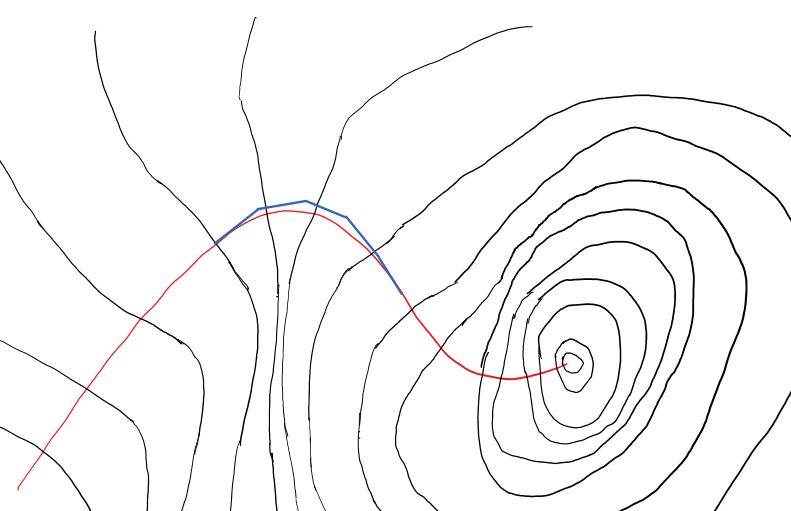
这时候我们发现bgd的蓝色路径其实和最速下降线的路径存在差异,这个差异会随着学习速率的增加而越来越明显。只有当学习速率趋向于0的时候,bgd路径与最速下降路径才能重叠。
事实上,在一轮迭代前进的线段内,除了起始点以外,其他任何点的bgd梯度都和切线存在不同,$\zeta_{bgd}(\boldsymbol{w})=0$只在每条线段的起始点为真。一旦对蓝色bgd路径上的噪音进行积分,就可以看到$\xi_{bgd}=\frac {1} {S} \int\limits_{s \in BGDPath} \zeta(\boldsymbol{w})ds = \epsilon > 0$会是一个比sgd噪音小得多,但不为0的正数。
这也解释了为什么即使是bgd,也能观测到不是很明显的互信息I(T, X)压缩了。
总结一下训练过程的原则:
我们可以用寻找海拔最低点的任务来类比一下优化问题,首先有几个限制条件:
1. 没有精确地图(真实分布等高线)的知识,掌握的只有历史经过的路径的知识。
2. 自身携带的海拔测量器的精度与原地测量时间呈正比,要靠实地计算来找准梯度下降的方向,就需要增加信噪比,无论减少lr还是增加batch size,付出的代价都是时间。
3. 测量自身海拔时必须原地不动,但是一旦决定好下一个目的地坐标,可以瞬间移动过去。也就是说赶路的时间永远是O(1),主要的时间花费在测量海拔上。
任务目标是,用最短的时间,从起点开始,找到地图上的最低点,而且最好能对局部最优解有一定的免疫力。
无论sgd、bgd、momentum,还是adam,都是在这样一套规则下,使用不同策略来实现同样的目标的手段。
高效一些的策略可以是在刚开始大范围内选取若干个起始点,大步长、粗精度测量,找出一些可能存在全局最优的区域,随后保留这些区域附近的下降路线,删除其他路线。之后通过增加batch size以及减小步长,增加信噪比,获得更精确的海拔与梯度方向测量。
不断重复删除不好的路径,对较好的路径进行更精确的下降,最终可以用相对较小的时间代价找到全局最优。
搅局的范化误差
前面所有的推理,都是基于一个假设,即经验风险等于期望风险,$L_{emp}(\boldsymbol {w})=L(\boldsymbol {w})$
然而实际情况下,这个假设很多时候并不成立。也就是说你拥有的海拔测量器实际上存在系统误差,花费大量时间精确测量的-200米,实际上是-199米,然后旁边测量出-199.5米的地方,实际上是-200.5米。带来的问题就是范化误差,其根源是有限的训练集样本与预测集样本分布的不一致。
根据机器学习$error = bias^{2} + variance + noise$的原则,这里的noise不同于前面提到的noise,而是范化误差下界,即不可避免的那部分noise。前面提到的信噪比的noise实际上是$variance+noise$。bgd里预测集分布未知且只有一个训练集,实际上就是mini-batch机制的一个特殊情况,即不允许重新采样,导致“variance”的部分无法被正确统计,让我们误以为bgd时variance已经是0了,泛化下界反正来源于H(Y|X),无法消除就干脆忽略不计,所以bgd的梯度就没噪音了,只需要迭代优化参数降低bias就行了。但如果我们开启上帝视角,允许从预测集中多采集几套训练集,那么就能获得更加接近真实的batch size=N时的非零variance。这时候甚至会发现上帝视角非零variance实际上比bias要更大,构成了范化误差的主体。
这时候我们就开始思考怎样获得更准确的variance了。无论sgd还是把bgd训练集切分成若干个train和validation的cross-validation,实质上都是牺牲bias(让地图更加扭曲变形),但是换取更准确的variance(获得更多张不精确的地图的局部梯度,综合考虑它们指引的方向)的做法。
在任何一个训练集看来,任何其他独立采集出的,与自身采集不相关的mini batch所计算出的梯度,都和噪音无异。只有站在上帝视角,能够得知真实分布的最速下降线路径的观测者,才能通过计算梯度方向与最速下降线方向的内积,知道一个mini batch计算出的梯度里究竟包含的信号与噪音各占多少。而真实训练里,我们只能选取精确bias与精确variance中间的一个平衡,然后最小化它们一同组成的error,最终相信它能够在预测集里取得较好的表现。
范化误差上界的推导在前面的博客中有证明。结论是除了增加训练样本集大小之外,减少隐藏层包含的信息熵也能降低范化误差的上界。
再结合“增加噪音能够压缩隐层与输入的互信息”的结论,基本上可以得到这样一个直观解释:
给前进的方向增加了些许不确定性之后,那么在最终收敛的小范围附近时,使用错误的variance(尤其是bgd的variance=0)算出的梯度信号减弱,顺着带有【相对正确一些的variance】的“噪音”的方向指引,最终反映出的位置预期概率最大的地方,反而比经验风险最小的无噪音指引目标更接近全局最优,从而降低范化误差。
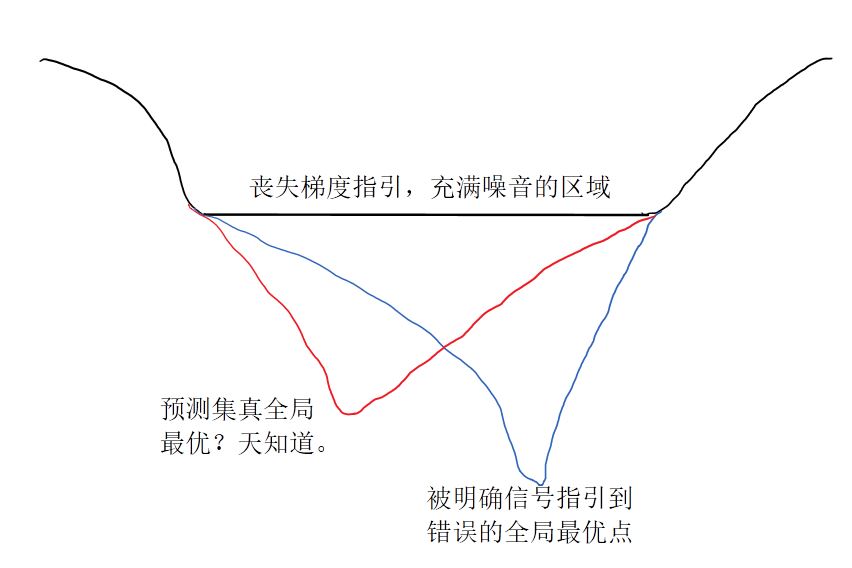
虽然不是上帝视角,不知道“噪音”中有多少是variance,多少是noise,但正是混杂在“噪音”中的variance也能被正确评估了,并在随机梯度下降过程中作为error的一部分被一同最小化,范化误差的上界才能被降低,根据公式也必然导致H(T)里面属于I(T, Y)那部分的信息被压缩。
同时H(Y|X)这部分设置了范化误差的下界,无论variance能被优化到多低,H(T)有多接近I(T, Y),都不会影响error公式里noise这部分。
