重构self-attention
Self-attention机制,在深度学习中的各个方面都取得了巨大的成功。很长时间以来我一直以为其关键的核心在于softmax的注意力权重分配,直到几个月前仔细思索了一番,才理解到它的核心在于同级别表征向量之间的“相互作用”。
\begin{equation}
a_{ij}=\left\{
\begin{array}{rcl}
J & & {D(q_i, k_j) \leq R}\\
0 & & {D(q_i, k_j) > R}
\end{array}
\right.
\label{XX}
\end{equation}
简单粗暴的方法,就是如果$q_i$与$k_j$在经过某个度量函数D之后(可能包含一些可训练参数),计算出的度量距离小于一个固定门槛R,就给一个非0的常量注意力权重。否则注意力为0。因为度量距离函数的输出是被可训练参数影响的,所以可训练参数决定了流形空间的形状,能够修改邻居的成员构成。由于在平整的value相空间内,有些邻居的距离在修改之前本身很大,所以流形的本质功能是赋予了远距离交互作用的能力。
$h_i=\sum\limits_{j | D_{ij} \le R} a_{ij} v_j$,每个向量i可以看作一个磁针,与半径R以内的相似“邻居”发生交互作用,使得i的指向变成它与邻居们的平均值。当每个磁针i都执行这样的操作后,实际上就是磁针阵列中真实发生的情况。
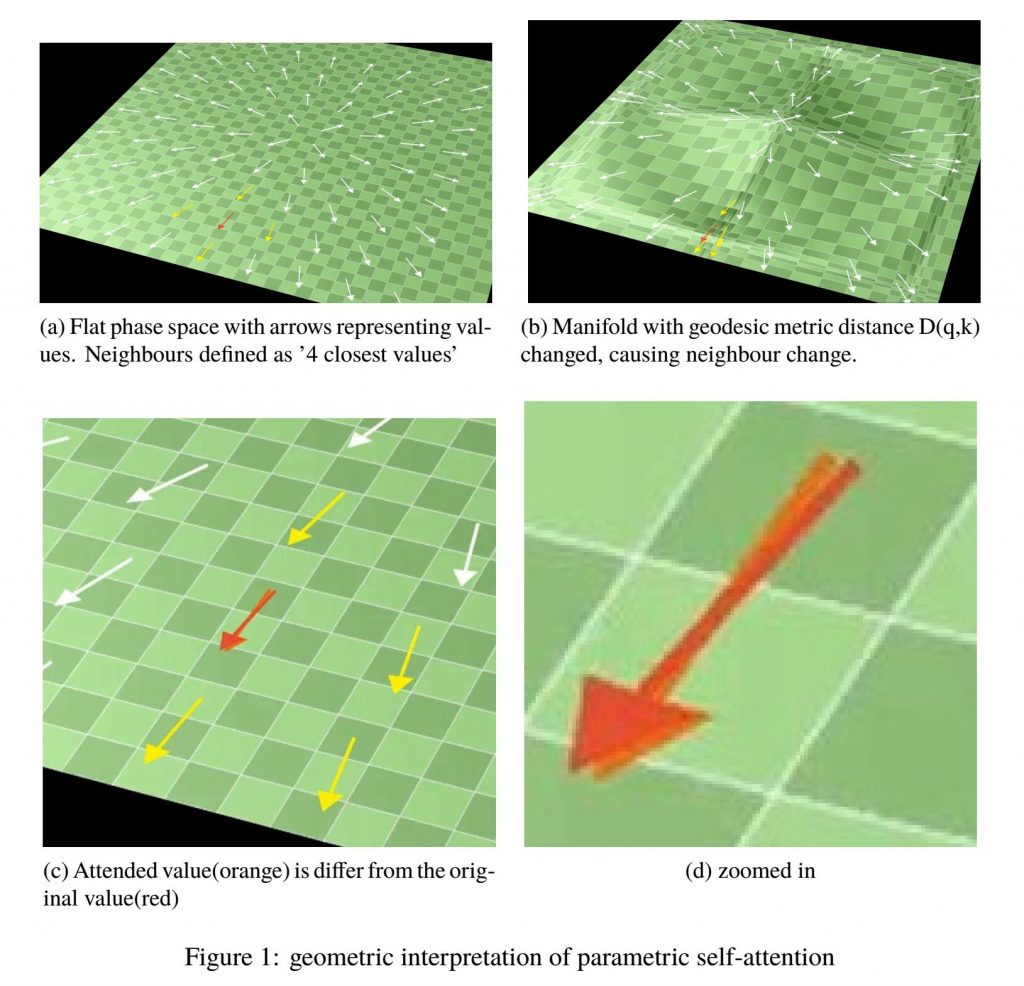
上图描述了当“邻居”的定义是“4个最相似的其他向量”时,注意后的输出,在使用了非线性核(自定义度量距离公式)的流形交互作用后,与原本默认线性核时的该变量差异。这种交互作用机制就是self-attention的几何解释。
使用Ising模型能够对这样一批向量进行建模。Hamiltonian的形式猜测是这样的:
\begin{equation}
H=-\sum\limits_{i,j} a_{ij} q_i k_j – \sum\limits_{i}B_{ext} q_i
\label{HAMT}
\end{equation}
1维自由度的平均场分析里,$q_i$与$k_j$的位置上都应该是标量,而非向量。换言之self-attention中的向量表征,需要被映射到一个标量上,映射函数 $f : \mathbb{R}^{(1)} \rightarrow \mathbb{R}^{(0)}$,之后再把映射后得到的标量离散化,四舍五入到$\{-1, +1\}$上。磁针只允许两个方向:“朝上”或是“朝下”。这一段离散化的必要性,以及$B_{ext}$究竟是什么,后面再解释。总之从“交互作用”的角度来理解的话,self-attention与ising模型是具有一些相同的作用机制的。
迭代结构
接下来回到self-attention公式里,发现$\boldsymbol{H}_{i}^{(1)}=\sum\limits_{j} a_{ij}^{(1)} \boldsymbol{V}_{j}^{(1)}$可以看作是感知器$y_i=\sum\limits_{j} w_{ij} x_j$的升阶。value V的上标与注意力输出H的上标(l)代表了他们都是l阶张量;标量权重$a_{ij}$的上标,则代表了公式\eqref{XX}中度量距离函数D的两个输入张量$q_i$和$k_j$的阶数。$a_{ij}^{(0)}=w_{ij}$是一个特殊情况,深度学习中0阶输入的度量距离函数并不是计算出的,而是从可训练矩阵w中查询对应位置得到的。
每次升阶,都涉及到一个聚合操作,例如将64*256个0阶标量聚合成64个1阶256向量。在深度学习中这种聚合操作是不重叠的,每个标量只能归属于1个向量。此外聚合成员的选择规则也是固定的,例如RNN中固定将同一个time step的标量聚合成一个向量,CNN中固定将同一个坐标位置的标量聚合成一个向量。当然这样的聚合规则也并非不可打破,实际上$l>1$时的聚合,也是允许根据相似度来选取聚合成员的。
使用$V_{j’}^{(l+1)}=AGG_{j’}(\boldsymbol{H}_{i}^{(l)})$来描述从i循环的低阶张量list中选取一定数量个成员,聚合成一个高阶张量,之后重复若干次,形成一个高阶张量list,用j’来循环的过程。
于是可以形成一个迭代嵌套,让张量聚合升阶的操作持续下去,形成一个迭代:
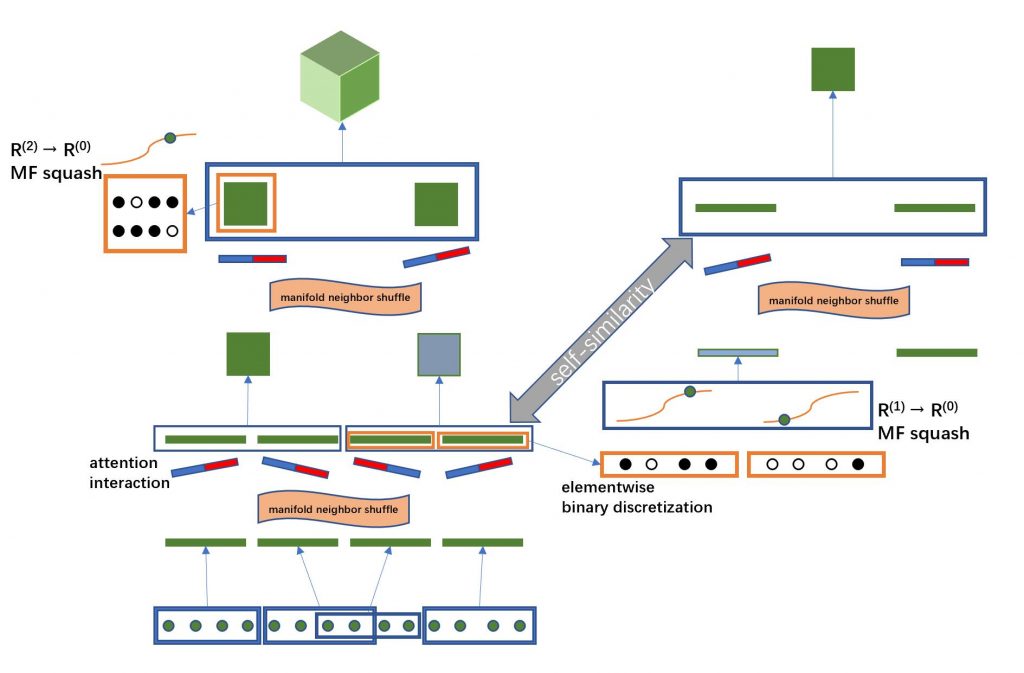
激活函数的形状计算比较繁琐,需要考虑\eqref{HAMT}作为Hamiltonian时离散化后磁针$p(s_i=1)$与$p(s_i=-1)$时的概率,再求出张量范围内的磁针预期值$\mathbb{E}[s_i]$,让它等同于张量内children元素在离散化之前的平均值$\bar{s_i}$,之后获得这样一个公式:
\begin{equation}
\bar{s} = tanh\left( \beta(\bar{n}J \bar{s} + B_{ext}) \right)
\label{MF2}
\end{equation}
其中标量$B_{ext}=\frac{1}{|H_i^{(l)}|}\sum\limits_{m \in H_i^{(l)}} f(H_{m}^{(l-1)}) + b$,是组成张量$H_i^{(l)}$的低阶成员被压缩成连续标量后的平均值,再加上一个常量bias。它是平均场的标量输入,与标量输出$\bar{s}$的关系构成了激活函数的形状。
J是\eqref{XX}中的常量,$\beta=\frac{1}{k_B T}$是与温度相关的常量。
最重要的一个参数是$\bar{n}$,是平均每个磁针的能够发生非0交互作用的“邻居”的数量。
解\eqref{MF2}的$\bar{s}$放在纵轴,$B_{ext}$放在横轴,得到激活函数的形状:
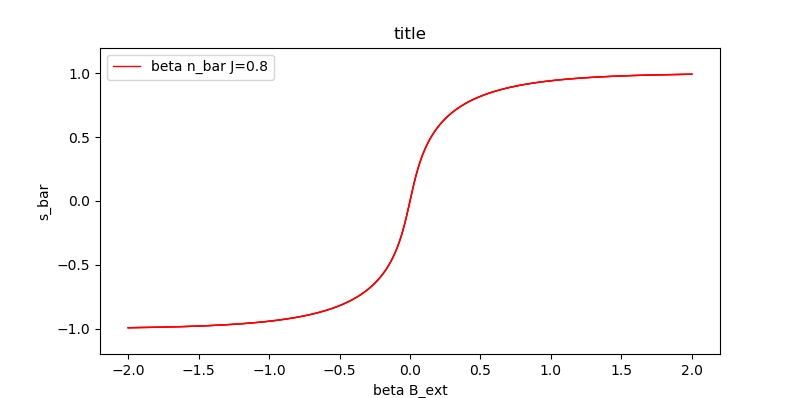
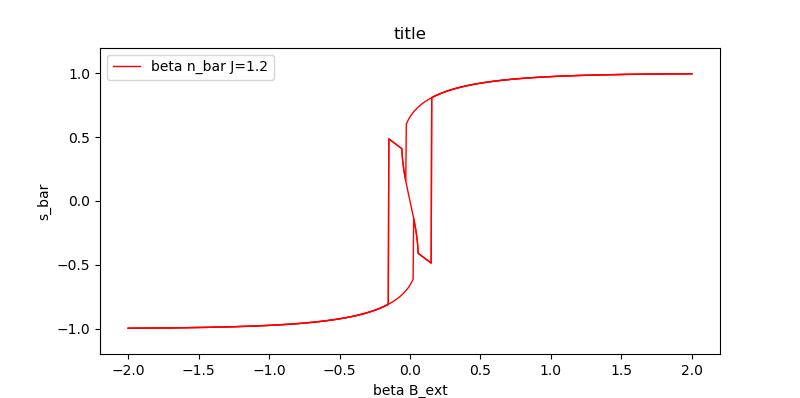
可以看出当平均邻居数量较小,“磁针”之间的神经元连接密度不高时,激活函数是上面那个近似于tanh的曲线(其实并非tanh)。
当邻居数量较多,“磁针”之间神经元连接密度较大时,激活函数是下面有着奇怪形状并不算函数的东西。这个在电磁学中被称作“磁滞回线”,与磁铁中的相变相关。
相变现象在这里的表现形态是,当输入$B_{ext}$在某个靠近0的范围内时,只需要一点点变化,甚至连变化都不需要,就可以让输出产生非连续的且很明显的改变。
如果$\bar{n}$太小,那么2层迭代+激活函数的功能与现在的self-attention+tanh激活函数几乎没有区别。现有的深度学习理论可以解释它的原理以及功能,并不在我们讨论的范围内。新产生的有趣现象发生在能够产生相变的时候。
$\bar{n}$的大小,除了影响磁滞回线和激活函数的形状外,还与脑科学中的很多现象有关。
一个张量内发生相变的后果,与迭代了很多层的整个网络内如果发生了相变的传导,会产生什么样的后果,会非常有趣。
下篇文章会讨论相变和复杂系统,以及与脑科学的很多关联。
