考虑一个简单的感知器,输出标量y:$y = \boldsymbol{x}^T \boldsymbol{w}$
让数包含n个样本的据集写为$\boldsymbol{A}=[\boldsymbol{x}_1, \boldsymbol{x}_2, … \boldsymbol{x}_n] \in \mathbb{R}^{(m, n)}$
把target写作$\boldsymbol{t} = \left[t_1, t_2, …, t_n\right]^T$,则根据最小二乘loss:
$J = \frac {1}{2} (\boldsymbol{t} – \boldsymbol{A}^T \boldsymbol{w})^T (\boldsymbol{t} – \boldsymbol{A}^T \boldsymbol{w})$
梯度$\frac {\partial J} {\partial \boldsymbol{w}} = (\boldsymbol{A} \boldsymbol{A}^T) \boldsymbol{w} – \boldsymbol{A} \boldsymbol{t}$
解存在于$\boldsymbol{w}^* = (\boldsymbol{A} \boldsymbol{A}^T)^{-1} \boldsymbol{A} \boldsymbol{t}$
加入L2正则项$\alpha \boldsymbol{w}^T \boldsymbol{w} $,使得求inverse matrix时避免$det|\boldsymbol{A}| = 0$,解变成了
$\boldsymbol{w}^* = (\boldsymbol{A} \boldsymbol{A}^T + \alpha \boldsymbol{I})^{-1} \boldsymbol{A} \boldsymbol{t}$
针对inverse matrix部分,使用Sherman-Morrison Formula
$\boldsymbol{\Phi}^{-1}(n+1) = (\boldsymbol{\Phi}(n) + \boldsymbol{u}\boldsymbol{v}^T)^{-1} = \boldsymbol{\Phi} ^{-1}(n) – \frac {\boldsymbol{\Phi} ^{-1}(n) \boldsymbol{u} \boldsymbol{v}^T \boldsymbol{\Phi} ^{-1}(n) } { 1 + \boldsymbol{v}^T \boldsymbol{\Phi} ^{-1}(n) \boldsymbol{u}}$
每次新增一条样本$\boldsymbol{u} = \boldsymbol{v} = \boldsymbol{x}_{n+1}$时,$\boldsymbol{\Phi}^{-1}$都可以被增量更新,其中
$\boldsymbol{\Phi}(0) = \alpha \boldsymbol{I}$
$\boldsymbol{\Phi} (n) = \boldsymbol{A}(n)\boldsymbol{A}^T(n) + \alpha \boldsymbol{I} =\sum\limits_{i=1}^n \boldsymbol{x}_i \boldsymbol{x}_i^T + \alpha \boldsymbol{I} = \boldsymbol{\Phi}(n-1) + \boldsymbol{x}_n \boldsymbol{x}_n^T$
针对后面的At部分,$\boldsymbol{A}(n+1) \boldsymbol{t}(n+1) = \boldsymbol{A}(n) \boldsymbol{t}(n) + t_{n+1} \boldsymbol{x}_{n+1}$
新增一条样本时,新的权重应该是
\begin{equation}
\boldsymbol{w}^*(n+1) = \left( \boldsymbol{\Phi}(n) ^{-1} – \frac {\boldsymbol{\Phi}(n)^{-1} \boldsymbol{x}_{n+1} \boldsymbol{x}_{n+1}^T \boldsymbol{\Phi}(n) ^{-1} } { 1 + \boldsymbol{x}_{n+1}^T \boldsymbol{\Phi}(n) ^{-1} \boldsymbol{x}_{n+1}} \right) \left( \boldsymbol{A}(n) \boldsymbol{t}(n) + t_{n+1}\boldsymbol{x}_{n+1} \right)
\label{eq1}
\end{equation}
$=\boldsymbol{\Phi}(n+1)^{-1} (\boldsymbol{A} \boldsymbol{A}^T \boldsymbol{w}^{*}(n) + t_{n+1} \boldsymbol{x}_{n+1})$
$=\boldsymbol{\Phi}(n+1)^{-1} \left[ (\boldsymbol{\Phi}(n+1) – \boldsymbol{x}_{n+1}\boldsymbol{x}_{n+1}^T) \boldsymbol{w}^{*}(n) + t_{n+1}\boldsymbol{x}_{n+1}\right]$
$=\boldsymbol{w}^{*}(n) + \boldsymbol{\Phi}(n+1)^{-1} \left[ \boldsymbol{x}_{n+1} (t_{n+1} – \boldsymbol{x}_{n+1}^T \boldsymbol{w}^*(n)) \right]$
注意到方括号里正是使用上一轮的参数解,在新样本$\boldsymbol{x}_{n+1}$上计算的梯度$\frac{\partial J} {\partial \boldsymbol{w}} \mid_{\boldsymbol{w}=\boldsymbol{w}^*(n)}$
所以不会导致过去已学习到的知识丢失的梯度更新方向应该是
\begin{equation}
\boldsymbol{w}^*(n+1) – \boldsymbol{w}^*(n) = \kappa \boldsymbol{\Phi}(n+1)^{-1} \frac{\partial J} {\partial \boldsymbol{w}} \mid_{\boldsymbol{w}=\boldsymbol{w}^*(n)}
\label{eq2}
\end{equation}
其中$\boldsymbol{\Phi}(n+1)^{-1}$的增量更新方法参见\eqref{eq1}右边的第一个括号;$\kappa$是学习速率
论文《Continual learning of context-dependent processing in neural networks》中的OWM正是基于这样的原理设计的。
基本思路是每完成一个分类的所有样本的mini-batch的训练后,增量更新$ \boldsymbol{\Phi}(k+1)^{-1} = \boldsymbol{\Phi}(k)^{-1} – \frac { \boldsymbol{\Phi}(k)^{-1} \bar{\boldsymbol{x}} \bar{\boldsymbol{x}}^T \boldsymbol{\Phi}(k)^{-1} } { 1 + \bar{\boldsymbol{x}}^T \boldsymbol{\Phi}(k)^{-1} \bar{\boldsymbol{x}} }$
k=range(分类数量)而非range(样本数量),每次训练完一个分类后,才更新最优解空间的projector
$\boldsymbol{P}(k) = \boldsymbol{\Phi}(k)^{-1}$
仍然存在一个问题,就是每个mini-batch必须把完整的一个分类里的所有样本一次性输入,所以论文里使用了一个trick,就是把一个分类拆成多个mini-batch,然后假装每个mini-batch都是一个单独的类别。
$\bar{\boldsymbol{x}} = AVG(\boldsymbol{x} \in \text{MiniBatch})$
每个样本在当前层的特征,被计算了mini-batch内的均值再用于batch增量更新,这里可能会引起一些问题导致模型效果降低。
要进一步理解projector $\boldsymbol{P}$的作用,需要使用reduced QR分解。
可以把$\boldsymbol{A} \in \mathbb{R}^{(m,n)}$分解为一个正交基矩阵$\boldsymbol{Q} \in \mathbb{R}^{(m,m)}$和一个上三角矩阵$\boldsymbol{R} \in \mathbb{R}^{(m,n)}$:
$\boldsymbol{A} = \boldsymbol{Q} \boldsymbol{R}$
只有当$n \le m$时才能确保每次新增一个样本时,只有该新样本能够有一个新的正交与已有基的unit vector上出现非0投影。
$\boldsymbol{A}[:, j] = \sum\limits_{i =0}^{i \le j} r_{ij} \boldsymbol{q}_i = \boldsymbol{x}_j$
$\boldsymbol{Q} = [\boldsymbol{q}_1, \boldsymbol{q}_2, … \boldsymbol{q}_m]$
原本的$\{ \boldsymbol{x}_i \in \mathbb{R}^{(m)} \}$可以看作是一套非正交的基,要用一套新的正交基$\{\boldsymbol{q}_i \in \mathbb{R}^{(m)} \}$来取代,并找到$\boldsymbol{q}_i(\boldsymbol{x}_1, \boldsymbol{x}_2, … \boldsymbol{x}_m)$的映射关系。这里m个x基实际上是把n的上限降下来,以确保under-determined不会出现,即保证$m \ge n$。
使用Gram-Schmidt正交化方法,即
$\boldsymbol{b}_1 := \boldsymbol{x}_1 $
$\boldsymbol{b}_i := \boldsymbol{x}_i – \sum\limits_{j=1}^{i-1} \frac {\boldsymbol{x}_i^T \boldsymbol{b}_j } { \boldsymbol{b}_j^T \boldsymbol{b}_j} \boldsymbol{b}_j$
$\forall i > 1$
把b归一化成unit vector可得$\boldsymbol{q}_i := \frac {\boldsymbol{b}_i} {|| \boldsymbol{b}_i ||}$
则存在$\boldsymbol{x}_i = \sum\limits_{j=1}^{i} r_{ij} \boldsymbol{q}_j$,$r_{ij}=\boldsymbol{x}_i^T \boldsymbol{q}_j$
以矩阵形式:
$$
\left(\boldsymbol{x}_1, …, \boldsymbol{x}_m \right) = \left( \boldsymbol{q}_1, …, \boldsymbol{q}_m \right) \left[
\begin{array} {cccc}
r_{11} & r_{12} & … &r_{1m} \\
& r_{22} & … & r_{2m} \\
& & … & … \\
& & & r_{mm} \\
\end{array}
\right]
$$
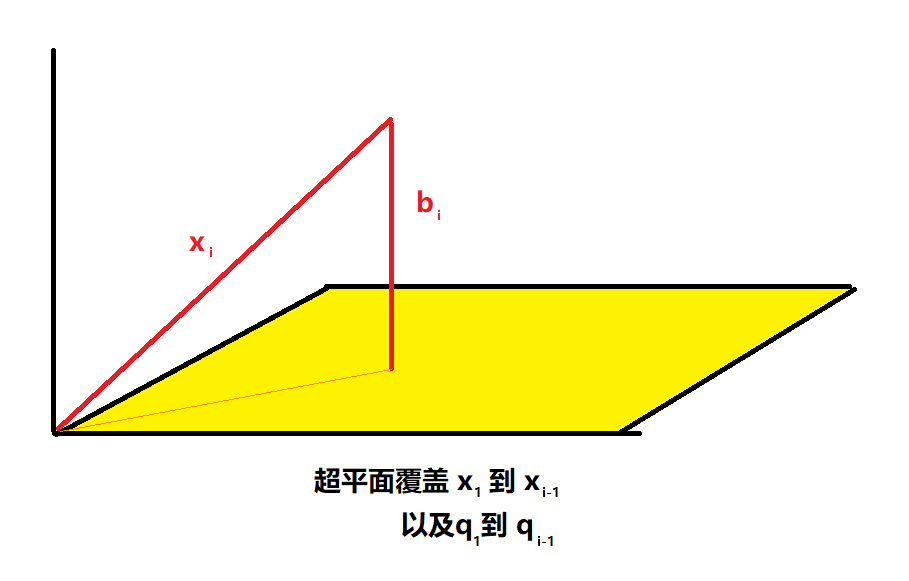
$\boldsymbol{b}$的定义确保了无论第几次增加样本数量,都能让最新增加的第i个样本$\boldsymbol{x}_i$拥有垂直于所有已有的样本在已被占用的正交基$(\boldsymbol{q}_1, …\boldsymbol{q}_{i-1})$形成的超平面的新unit vector,即$\boldsymbol{q}_i$ 上的非0投影。
上三角的inverse也是上三角,让
$$
\boldsymbol{D} = \left[
\begin{array} {cccc}
r_{11} & r_{12} & … &r_{1m} \\
& r_{22} & … & r_{2m} \\
& & … & … \\
& & & r_{mm} \\
\end{array}
\right]^{-1} = \left[
\begin{array} {cccc}
d_{11} & d_{12} & … &d_{1m} \\
& d_{22} & … & d_{2m} \\
& & … & … \\
& & & d_{mm} \\
\end{array}
\right]
$$
\eqref{eq2}进行梯度更新时,使用了一个变换后的梯度g’来进行梯度下降$\boldsymbol{g}’ =\boldsymbol{\Phi}(n+1)^{-1} \boldsymbol{g}$,使用QR分解,Q正交,R上三角可得:
$\boldsymbol{g}’ = (\boldsymbol{Q}\boldsymbol{R}\boldsymbol{R}^T \boldsymbol{Q}^T)^{-1} \boldsymbol{g}$
$ \boldsymbol{R}^T \boldsymbol{Q}^T \boldsymbol{g}’ = \boldsymbol{D}^T \boldsymbol{Q}^T \boldsymbol{g}$
可以看作是把原先的$\boldsymbol{w}$和$\boldsymbol{x}$所在的空间变换到了一套正交基$\boldsymbol{Q}$的空间内,使得最新的第i个batch的梯度是唯一在$\boldsymbol{q}_i$基的方向存在非0投影。之后利用Transpose得到的下三角矩阵的特性,对第i个batch的输入只允许在$j \le i$的$\boldsymbol{q}_j$方向上产生修改,从而实现在不破坏每个样本都有它唯一专属的非0投影基的前提下进行变换。
这样一来任何旧样本的输入$\boldsymbol{x}$以及它们训练出的权重$\boldsymbol{w}$在经过上述转换后,都会垂直于最新一个batch对应的基$\boldsymbol{q}$,从而导致计算$y=\boldsymbol{w}^T(\sum\limits_{j=1}^{i} r_{ij} \boldsymbol{q}_j)$时,在最新的基方向上$\boldsymbol{w}^T \boldsymbol{q}_i = 0$,不会影响旧batch的y值,也就不会影响旧类别的模型效果。
