之前的文章已经阐述了self-attention与ising模型的磁偶极子交互作用之间的等价关联。Transformer中的self-attention本质上也是在进行同样的交互作用,但是有别于ising模型中,交互存在于同一时间的不同的几何空间的位置之间,transformer的交互更像是把时间转换成了几何空间之后的ising模型。Ising模型的超距离交互,在transformer中变成了穿越时间的交互。
为了说明上面的结论,先回到transformer的编码部分的基本结构来,用直白一些的话语来表示如下:
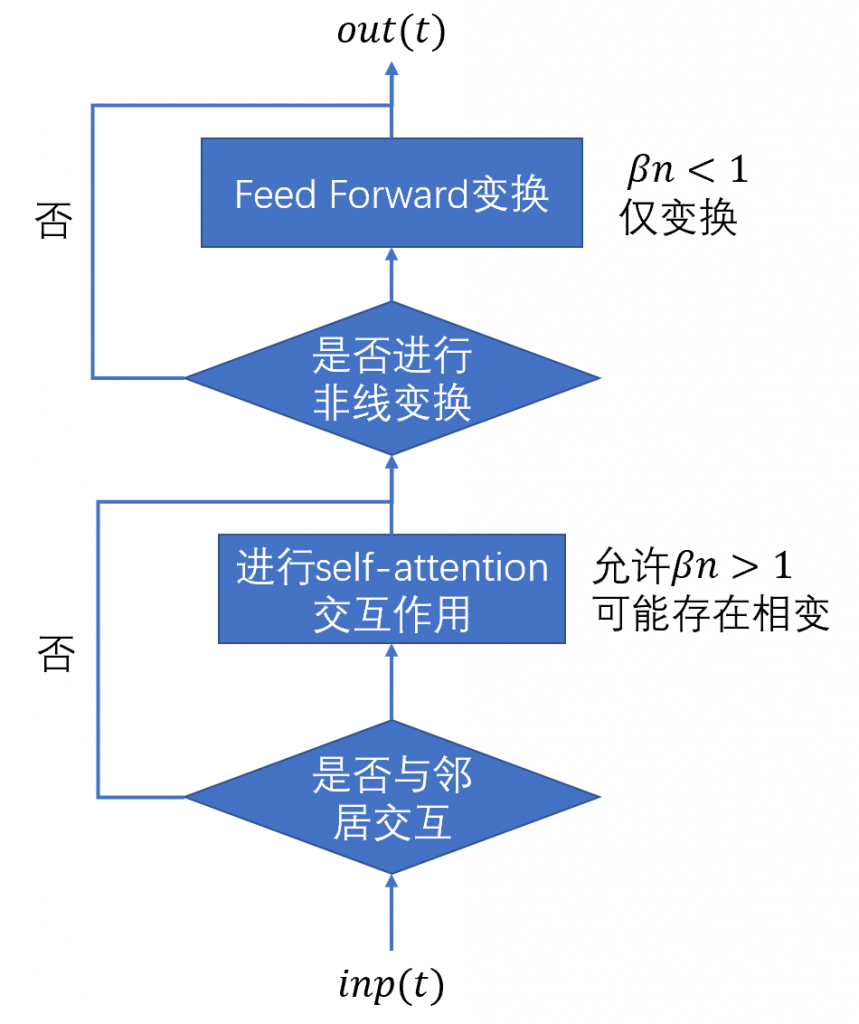
输入信号理论上可以在self-attention时以及FF时都利用residual操作绕开变换,使得$out(t)=inp(t)$,同时也可能被self-attention模块或是FF模块又或是被两者同时变换。如果按照前文中提到的平均场方法,self-attention模块只要解除attention权重必须归一化的限制,密集的交互作用会导致$\beta n > 1$,从而造成相变。而FF模块的非线性变换相当于一个$\beta n < 1$的平均场。所以一个transformer单元理论上可以是一个覆盖了“强交互强信息压缩”、“弱交互非线性变换弱信息压缩”、“信息无损传导” 这三种功能的变换单元。
接下来考虑时间序列上的“穿越交互作用”现象。
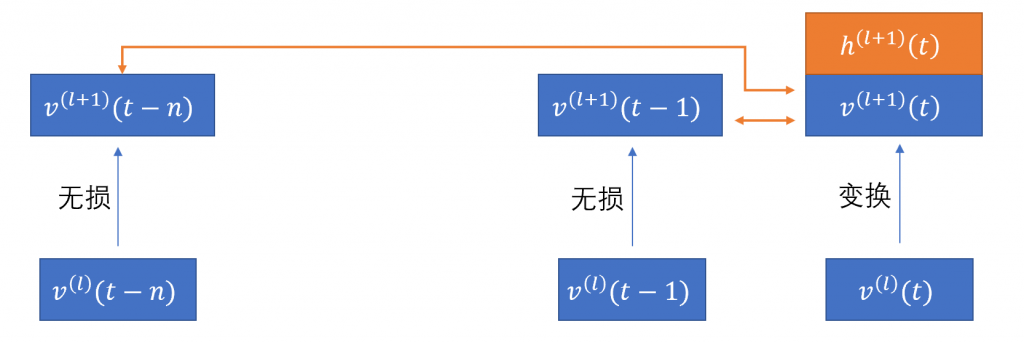
假设某个时间t,(l+1)层的transformer都能实时处理并变换当前的从第l层获得的输入信号。
而在上一个时间点(t-1)上,transformer决定的处理结果是“信息无损传导”,那么在t时刻进行的self-attention机制里,就需要与(t-1)时曾经处理过的输入信号进行query-key对比计算。
举个例子,就是昨天的我画了一朵花,然后把画交给了邮递员。第二天我又画了一朵花,因为输入的心情不同所以与第一天的画会有些许不一样。同时昨天的邮递员邮递员用了一天的时间绕了一个小圈,把我昨天的画又送回了我手上,这样我就可以对比两天的画,计算相似度以及attention权重。同理我也可以在今天收到n天前自己寄出的画,n天前的邮递员绕路更远,所以用的天数比较多。
如果存在空间上的“他者”,我可以把收件人设置成其他人,并指定邮递员送达的时间(NLP常用的编码里一个时间点只有一个向量表征,所以只能寄给自己)。邮递员在运输的过程中也可能出现失误导致画出现污渍或是破损,又或是画破损后邮递员寄到了别人手上,于是他修补好了并在画上添加了几笔,又把画寄给我。总之运输途中的画可能发生各种各样的事情。
以上出现的所有状况,都能够用几层transformer来描述。BERT中12层transformer意味着一幅画最多可以被转手12次,每次转手间隔至少需一天,每次转手可能产生“强信息压缩二值化”、“弱信息压缩非线性变换”和“无损传导”三种事件中的任意一种。
这时已经可以看出BERT其实能够模拟SNN里动力学传播的特征,只不过信号的接收方只能是“过去”或是“未来”的自己。
假设信号传递的速度是固定的,那么经历了更长的神经传导路径的信号花费的时间就更久。
让时间变成连续值,transformer的瞬时输入信号(还来不及进行attention交互)是$q(t)$,经过邮递员转手$\tau$天后的信号变成了$k(\tau)$,那么卷积$(q * k)(t) =\int_{\tau =0}^{\tau \le t} \boldsymbol{q}^T(t) \boldsymbol{k}(t-\tau) d\tau$就是一种冲击响应函数,能够描述网络瞬时输出获得到的来自于其他“邮递员路径”的信号的支持程度。这个卷积的大小就代表了当前瞬时信号被激发作为一个事件而言的因果逻辑自洽性。
无论是平均场还是attention机制,交互后造成的结果是query与和自身相似的keys趋向于达成一致。瞬时信号作为query $\boldsymbol{q}(t)$,本质上就是按照最短激活路径到达的信号(不经过任何邮递员绕路)。所有花费了时间$\tau^*$绕了路的其他路径的信号$\boldsymbol{k}(\tau^*)$如果与$\boldsymbol{q}(t)$足够相似,则在附近范围$\tau=\tau^* \pm \epsilon$会产生较大的$(q * k)(t)$卷积贡献。反之也会存在一些负贡献的路径时间以及0贡献的路径时间。
根据用进废退机制,正贡献的路径上的连接会被强化,负贡献路径上所有与query相连的连接会被断开,以确保“逻辑自洽”卷积的值尽量大。假如交互作用时信号的模固定不变,只有方向改变,则最大卷积在query与“附近相似的”keys方向一致时达成。
为了说明为什么“相同到达时间的路径”这个概念很重要,假设这样一个场景:
每个时间点,一个transformer能够发射固定信号强度$|\boldsymbol{q}(t)| = 1$的信号,信号可以选择任意长度的路径传播。经过一些非线性变化后信号的模保持不变,但方向被调整,使得信号到达接收者的时候方向都基本上相同(类似ising磁针交互后指向相同)。发射持续10个单位的时间。
对比两种策略:
- 每次信号都沿最短路径传达至接受者手上,则$\boldsymbol{k}(\tau)= \boldsymbol{1} = const$。卷积$(q * k)(10)=\sum\limits_{\tau=1}^{10} \boldsymbol{1}^T\boldsymbol{1} = 10$
- 每次信号不按照最短路径,而是选择一条耗时=10-t的路径,以确保所有信号在第10秒同时到达接受者手上。这时卷积$(q * k)(10)=(\sum\limits_{\tau=1}^{9} \boldsymbol{10}^T \boldsymbol{0}) + \boldsymbol{10}^T\boldsymbol{10} = 100 $
当然神经元每次发射的信号数量不限于1个,且至少会有1个信号沿最短路径传递,但如果神经元或社区的连接方式能够使得针对任意接收者而言,所有在$t$之前的历史信号在沿着可传导路径上花费一定传导时间后到达目标的时间尽量一致,就能够叠加出一个瞬时脉冲使得卷积$(q * k)(t)$最大化。
