一些比较散乱的论文研究以及自己的思考,为了解决样本缺乏时的训练。
《Rethinking the Value of Labels for Improving Class-Imbalanced Learning》论文探讨了在类别不均衡样本数量的数据集上,不均衡比例与错误率之间的关系。论文首先假设了两个相同$\sigma$的,均值不同的正态分布标量,作为两类样本。一个在不均衡样本下训练得到的存在bias的分类器$f_B$,在推理集合$\{\hat{X}_i\}_{i=1}^{\hat{n}}$上进行inference,得到两种分类结果的集合分别是$\{\hat{X}_i^{+}\}_{i=1}^{\hat{n}_+}$与$\{\hat{X}_i^{-}\}_{i=1}^{\hat{n}_-}$,对于这两个集合,分类器是会呈现出准确率差异的。当预测准确时,$\mu_1$与+对应,$\mu_2$与-对应;而当预测错误时某个预测为+的样本实际上来自一个非$\mu_1$中心的正态分布$\hat{X}_i^{+} \sim N(\mu_{\neg 1}, \sigma)$。
训练后的模型估计$\hat{\mu}_1 =\sum\limits_{i=1}^{\hat{n}_+} \frac {\hat{X}_i^{+}} {\hat{n}_+}$,则根据数据集训练出的分类器得到的区分平面最优解应该在$\hat{\theta} = \frac {\hat{\mu}_1+ \hat{\mu}_2} {2}$的位置。
然而实际上真正的最优解位置应该位于真实$\mu$的中点,$\frac {\mu_1+ \mu_2} {2}$
对每一个预测的分类,+与-,定义某个样本i是否预测准确的指示器:
$I_i^{+}=1 \text{ or } 0 \sim Bernoulli(p)$
$I_i^{-}=1 \text{ or } 0 \sim Bernoulli(q)$
$p$与$q$分别是+与-分类下的分类器,在验证数据集上的准确率概率。根据定义,$\mu_1>\mu_2$,且p是样本较多的一方,预测准确率较高,两个准确率相差$\Delta := p-q$。
公式推导的结论是:
若$|\hat{\theta} – \frac{\mu_1+\mu_2} {2} – \Delta\frac{\mu_1-\mu_2} {2}| > \delta$ 对于任意$\delta>0$,该式满足的概率至少是
$1-2exp\{ -\frac{2\delta^2}{9\sigma^2}\frac{\hat{n}_+ \hat{n}_-} {\hat{n}_+ + \hat{n}_-} \} – 2 exp\{ -\frac{8n_+ \delta^2} {9(\mu_1-\mu_2)^2}\} – 2 exp\{ -\frac{8n_- \delta^2} {9(\mu_1-\mu_2)^2}\}$
得出两个结论:
- 保持$\delta$与公式满足置信概率不变时,$\Delta$越大时分界线$\hat{\theta}$越远离合理值$\frac{\mu_1 + \mu_2}{2}$,所以样本不均衡训练出的模型的分界线$\hat{\theta}$在真实数据上的表现越糟糕。
- 我们希望$\hat{\theta}$与$\frac{\mu_1 + \mu_2}{2}$尽量接近,在$\Delta$不变时,就要减小$\delta$。但要以相同的公式满足概率,也就是训练得到这样好的模型结果的概率保持不变的前提下减小$\delta$,就需要增加$n_-$与$n_+$,且$n_-$与$n_+$的比例最好均衡一些。
$n_-$和$n_+$是分类器$f_B$在无标注推理集合内获得的伪标签的个数,所以如果半监督学习时,要把伪标签当作真实标签放进模型一起训练,那么需要尽量多的未标注数据,且伪标签分布尽量均匀。
分类问题的相空间解释:
Cross Entropy里决定某个类别y的logits,计算如下$logits_{y}=\boldsymbol{h}_{fin} \cdot \boldsymbol{W}_{fin}\[y\]$
从最终层的权重$\boldsymbol{W}_{fin}$切下y位置上的向量,作为锚点,与样本的隐层输出去计算内积。
二维向量的内积等高线如下,更高维度的也是同样道理。
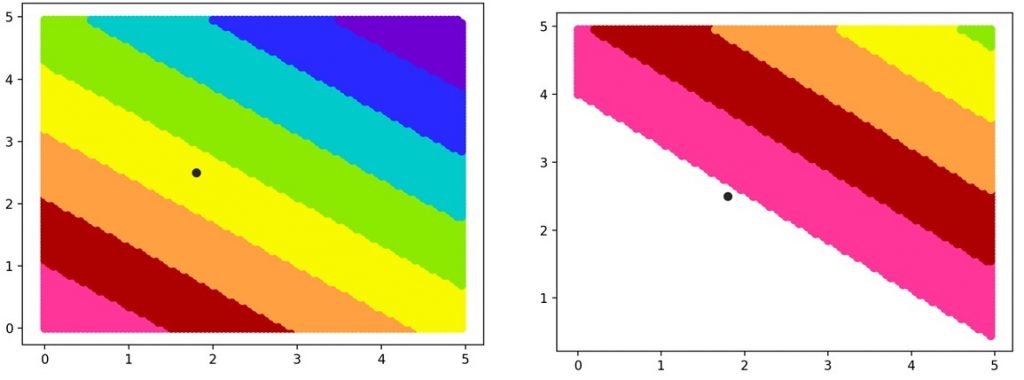
黑点是锚点的位置,左边是正常等高线,右图是添加了margin的等高线。
训练增加内积本质上是把正样本编码后隐层向量的位置往右上角黑点外的方向推,同时把负样本的编码向量往反方向左下角推。Margin可以让正负样本中间空出来一片区域用来更好地区分正负样本。
接下来看一下cosine相似度loss以及添加margin后的效果:
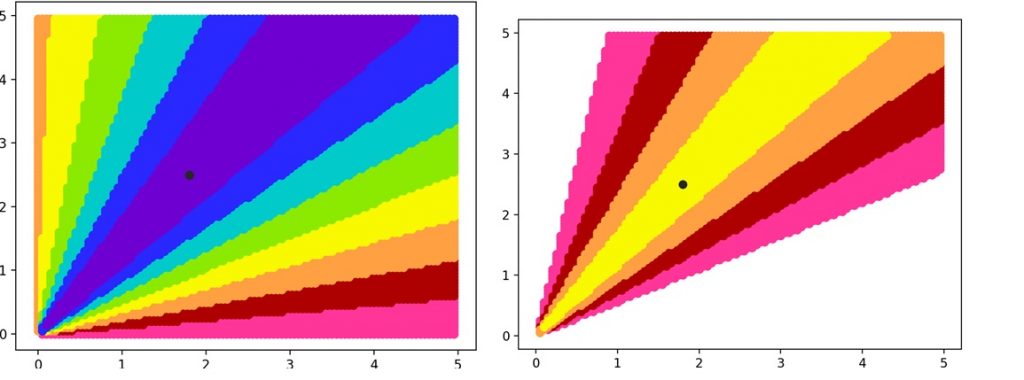
等高线的形状让正样本尽量往靠近锚点的角度位置靠近,同时让负样本远离锚点所在的角度。
结合Cross Entropy, cosine,以及L2正则项,综合起到的作用如下:
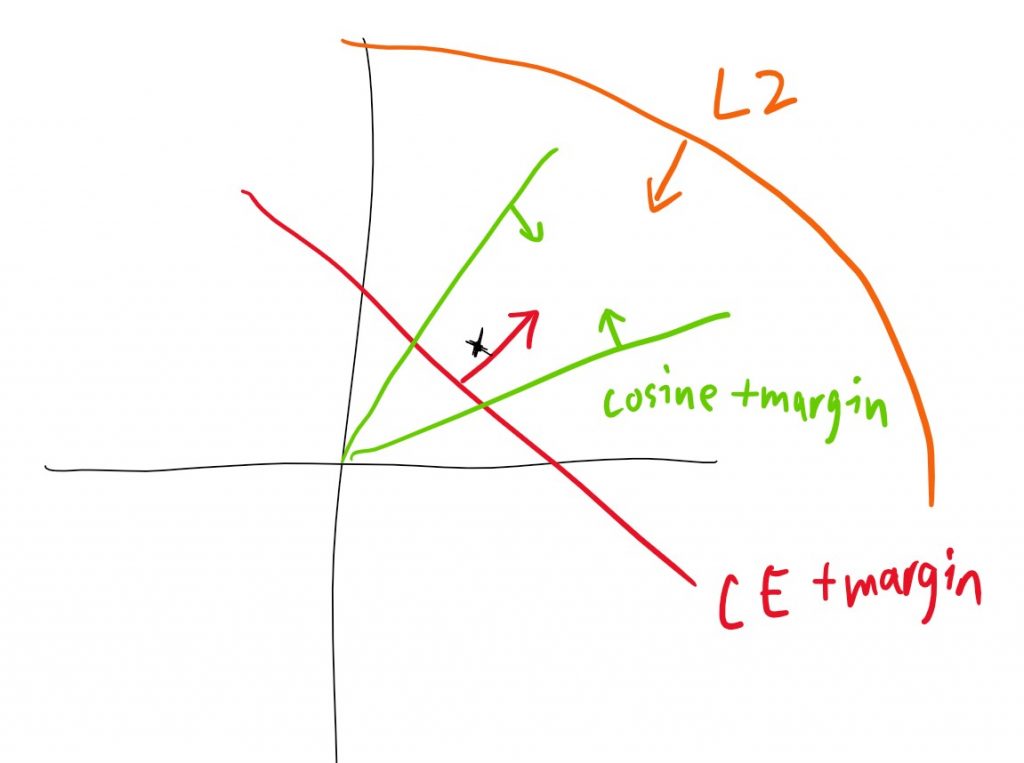
正样本会被三种loss限制在一个面积有限的区域附近,超出该区域都会造成较大惩罚,当然锚点位置也会随着训练而改变,对区域的位置造成一定影响。这也正是am-softmax损失函数的思路,已经非常接近metric-based learning的“类内距离减小”的聚类效果了。
分类模型与metric learning可以实现某种程度的迁移,理论上可以利用聚类以及metric learning缓解一些样本数量不足的问题。
OWM:orthogonal weights modification,具体见http://www.st-spacetime.com/index.php/2020/07/13/orthogonal-weights-modification/
GAN+半监督:编码器$h=Encoder(x)$;判别器$D(h_{lab/unlab})$判定是否是真实标记的样本;生成器$\hat{h}_{lab}=G(h_{unlab})$用来对未经标记的编码结果进行修正,使其尽量接近标注样本的编码。主要防止非标注以及标注数据集存在分布上的偏差,在训练初期就导致半监督的梯度下降跑偏。
