主动推断涉及到一些基础概念:
真实世界的演化机制过程,叫做generative process
智能体脑内建模,试图模拟真实世界的一套模型,叫做generative model
action分为两种,真实执行的$a$以及智能体假设在generative model内被执行的$u$
隐藏的不可观测的state s,是生成过程与生成模型的cause,也叫做control state。
智能体需要根据观测o来推测不同state的置信度(belief),即$q(s)$,用于后续generative model的推断以及产生action。
主动推断的Loss是free energy,以变分$F$表示。variational free energy与先验belief q的关系可以描述为:
$q(s) = \arg\max_{q} F \approx p(s \mid o_1, o_2, …, o_t) $
之前介绍变分推断的文章,描述了可以使用较少的参数$\nu$来推测隐变量$z$,作为真实状态$x$的一种简化代替描述,使得条件熵$H_{q}(Z \mid \mu)$与$H_{p}(Z \mid X)$在信息平面上尽量重叠。
然后通过琴声不等式$log(\mathbb{E}_{q}[p(x)]) \ge \mathbb{E}_{q}[log p(x)] = ELBO + KL[q(z \mid \nu)|| p(z \mid x)]$将左侧的log likelihood与它的下界(右侧ELBO)关联起来。
q是我们的简化模型近似出的真实分布p,$ELBO = \mathbb{E}_{q}[log p(z, x)] – \mathbb{E}_{q}[log q(z \mid \nu) ]$
x实际上是我们观测到的量,后面会用o来代指。
隐藏向量z是上帝视角才能看到的真实变量,后面会用s来代指。
如果按照贝叶斯的方式计算likelihood:$p(o)=\int\limits_{s} p(o \mid s) p(s) ds$,这个积分太复杂因为s的空间太大了,所以改为优化ELBO。
通过用一个prior belief $q(s \mid \nu)$来近似真实世界的$p(s \mid o)$,这两个分布的KL距离会随着ELBO的优化被挤压为0。
variational free energy的定义和ELBO是一样的
$F_{\tau} = \mathbb{E}_{q(s_{\tau})}[ -log q(s_{\tau}) + logp(s_{\tau}, o_{\tau})]$
$ = \mathbb{E}_{q(s_{\tau})}[ -log q(s_{\tau}) + logp(s_{\tau}) + logp(o_{\tau} \mid s_{\tau})]$
$ = D[q(s_{\tau}) || p(s_{\tau})] + \mathbb{E}_{q}[logp(o_{\tau} \mid s_{\tau})]$
第一项KL距离里两个分布分别来自prior belief与generative model,它们各自的输入依据被省略了,补全完整后是这样的
$F_{\tau} = F(o_{\tau}, q \mid \pi) = D[q(s_{\tau} \mid \nu, \pi) || p(s_{\tau} \mid s_{\tau-1}, \pi)] + \mathbb{E}_{q}[logp(o_{\tau} \mid s_{\tau})]$
时间累计下的variational free energy是
$F = \sum\limits_{\tau} F_{\tau}(\pi)$
F作为ELBO,也可以按照KL + log evidence的形式进行分解:
$F_{\tau} = \mathbb{E}_{q}[log q(s_{\tau}) – log p(s_{\tau}, o_{\tau})] = D[q(s) || p(s \mid o_{\tau})] – \mathbb{E}_{q}[log p(o_{\tau})] $
即$ELBO \le \mathbb{E}_{q}[log p(o_{\tau})]$的log evidence的下界描述。最大化ELBO也是在最大化log evidence。
要进一步揭示自由能的含义,考虑这个例子:
一只饥饿的猫头鹰,要寻找食物。
在强化学习里,被决定的action一般时是这样获得的:$u_t^*=\arg\max_{u_t} V(s_{t+1} \mid u_t) \sim \pi^*(s_t)$
V是value函数,不是评估当前轮状态,而是要推测下一轮s之后再评估,不考虑$\gamma$的话实际上等价于$Q(s, a)$
食物与reward挂钩,由一个客观上理应存在的Value函数用来指导猫头鹰接下来的动作。
但是实际上产生决策的步骤并没有那么简单。首先寻找是一个减少距离和方向不确定性的过程,不确定性这里指的是belief of state of the world的不确定性,即$q(s)$的某种熵或条件熵。于是搜索过程并非优化一个客观存在的value函数,而是在优化猫头鹰脑中的关于belief函数的变分,$G(q(s))$。这个变分的具体形式稍后会推导,与自由能相关。
优化后得到的policy $\pi^* = \arg\max_{\pi} \sum\limits_{t>now} G(q(s_t) \mid \pi )$,以及从该policy内产生的action $u^* \sim \pi^*(t)$
agent的驱动力从获取更高reward转化为了降低对未来世界状态的不确定性。reward的方式涉及到控制优化、DRL,基础是MDP里应用Bellman optimality equation。转化后的基础是Hamilton’s principle of stationary action,即物理中常见的最小作用量原理。物理里当很多物体相互作用,系统的自由维度过高时(可以理解为世界的隐藏状态s或是建模参数$\nu$的维度非常大),不可能对每个物体依次进行受力分析,去计算系统随时间的演化轨迹。
于是转而计算系统的Lagrangian,之后利用stationary action principle,写作$0 =\delta \int\limits_{t=t_1}^{t_2} L(q(s,t), t) dt$
求解该变分,可得函数q(s, t)随时间演化的轨迹。当然由于s过与庞大且需要上帝视角,所以人脑中实际是用参数$\nu$构建的脑内模型来估算得到q(s, t)。
这里的$\int\limits_{t} …dt$等同于前面的$\sum\limits_{t>now}$。
前面variational free energy仅需要一个轨迹$\widetilde{o}$即可计算,但如同强化学习里$Q(s, a)$一样,如果要想实现action selection,就需要扩展$V(s) \rightarrow Q(s, a)$,然后在计算预期时考虑policy。于是仿照F,重写一下考虑了策略后的未来自由能预期:
$\mathcal{F} = \mathbb{E}_{q(o_{\tau:T}, s_{\tau:T}, u_{\tau} \sim \pi)}[log p(o_{\tau:T}, s_{\tau:T}) – logq(s_{\tau:T}, u_{\tau:T})]$
序列action可以看作策略$\pi$生成的$\widetilde{u}$,所以式子里面的条件$\widetilde{u}$都用$\pi$代替了,虽然$\pi$不是一个端到端的模型,但它能通过一套固定的流程计算并产生$\widetilde{u}$
$q(s_{\tau:T}, u_{\tau:T}) = q(s_{\tau:T} \mid u_{\tau:T}) q(u_{\tau:T}) = \prod\limits_{\tau}^{T} q(s_{\tau} \mid u_{\tau}) \pi$
于是
$\mathcal{F} = \mathbb{E}_{\pi}\left[ \mathbb{E}_{q(o_{\tau:T}, s_{\tau:T} \mid \pi)}[ log p(o_{\tau:T}, s_{\tau:T}) – logq(s_{\tau:T} \mid \pi) – log\pi] \right]$
$ = – \mathbb{E}_{\pi}\left[ log \pi – \mathbb{E}_{q(o_{\tau:T}, s_{\tau:T} \mid \pi)}[ log p(o_{\tau:T}, s_{\tau:T}) – logq(s_{\tau:T} \mid \pi)] \right] $
$ = – D\left[\pi || e^{\sum\limits_{\tau}^{T} \mathbb{E}_{q(o_{\tau}, s_{\tau} \mid \pi)}[ logp(s_{\tau}, o_{\tau}) – logq(s_{\tau} \mid \pi) ] } \right]$
最大化上面的$\mathcal{F}$意味着策略$\pi$需要与一个softmax函数计算的分布一致,softmax的能量计算需要累加一个和variational free energy $F$非常像的预期:
$\mathbb{E}_{q(o_{\tau}, s_{\tau} \mid \pi)}[ logp(s_{\tau}, o_{\tau}) – logq(s_{\tau} \mid \pi) ] $
区别主要在于预期的prior概率是$q(o_{\tau}, s_{\tau} \mid \pi)$还是$q( s \mid \pi)$
从上面的预期,可以写出Expected Free energy的定义如下:
$$- G_{\tau}(\pi) = \mathbb{E}_{\widetilde{q}} [logq(s_{\tau} \mid \pi, \nu) – logp(s_{\tau}, o_{\tau} \mid \widetilde{o}, \pi)]$$
参数$\nu$只存在于近似先验分布$q$内,暂时简化省略。action $u \sim \pi$选自离散策略空间,$\tau$代表时间,$\widetilde{o}=(o_{1}, o_{2}, o_{3},…)$代表历史观测,s代表隐藏状态。p代表generative model中推测产生的概率,q代表与先验belief相关的,代表主观偏好。
$\widetilde{q}=q(o_{\tau}, s_{\tau} \mid \pi)=p(o_{\tau} \mid s_{\tau}) q(s_{\tau} \mid \pi) \approx p(o_{\tau}, s_{\tau} \mid \widetilde{o}, \pi)$,这里$q(o_{\tau} \mid s_{\tau}, \pi)=p(o_{\tau} \mid s_{\tau})$,是generative model中的一个模型,之后使用状态belief模型$q(s \mid \nu)=q(s)$作为prior,得到posterior $\widetilde{q}$。
对比ELBO的形态,可以看出最大化$G_{\tau}(\pi)$将会导致最大化$log p(o_{\tau} \mid \widetilde{o}, \pi)$。
最大化$\mathcal{F}$得到的策略$\pi$,是在当前时间$t_1=\tau$后推至$t_2=T$的时间范围里评估每种action的expected free energy $G_t$的累加,以此为依据,计算当前应该执行的action。那么要让$u_{t_1} \sim \pi(t_1)$更接近于纯策略,减少action的不确定性,就需要让$G(u)=\sum\limits_{\tau=t_1}^{t_2} G(\tau, u)$的值对于不同的u尽量要么最大化,要么最小化,产生足够的差异。softmax能量需要遵循principle of stationary action。 那么Lagrangian就对应了$G_{t}(q(s_{t}), \pi(t))$
接下来仔细分析一下$G_{\tau}(\pi)$的构成:
$-G_{\tau}(\pi) = \mathbb{E}_{\widetilde{q}}[log q(s_{\tau} \mid \pi) – log p(s_{\tau} \mid o_{\tau}, \widetilde{o}, \pi) – log p(o_{\tau})]$
$ \approx \mathbb{E}_{\widetilde{q}}[log q(s_{\tau} \mid \pi) – log q(s_{\tau} \mid o_{\tau}, \pi)] -\mathbb{E}_{\widetilde{q}}[log p(o_{\tau})] $
上面马尔可夫过程丢弃了历史观测,改用了一个近似分布。
第一项预期可转化为$- \mathbb{E}_{q(s, o)} [log \frac{ q(s, o \mid \pi)} {q(s \mid \pi) q(o \mid \pi)}] = -I(S; O)$。最大化G意味着增加观测与隐藏状态的互信息。也可以转化为$D[q(s \mid \pi) || p(s \mid o, \pi)]$,理解为按照某种策略执行之后得到的o,其hidden state额外带来了多少surprise。
第二项是-log evidence的预期,增加G也意味着log evidence的增加。
在推理$\tau > t_{now}$的过程里,如果generative model m的推理过程完全可见,s到o不存在模糊,$D[q(s_{\tau} \mid \pi) || p(s_{\tau})] = D[q(o_{\tau} \mid \pi) || p(o)]$那么这种情况下可以改写为:
$-G_{\tau}(\pi) \approx \mathbb{E}_{\widetilde{q}}[log q(o_{\tau} \mid \pi) – log q(o_{\tau} \mid s_{\tau}, \pi)] -\mathbb{E}_{\widetilde{q}}[log p(o_{\tau})] $
个人认为这里的转换不是很严谨,但论文中使用risk sensitive KL control的论点,原文说“Risk-sensitive or KL control works fine if there is no uncertainty or ambiguity about hidden states given observed outcomes. However, when the same state can lead to several outcomes (e.g., noisy or ambiguous cues), we have to augment the KL divergence with the expected entropy over outcomes given the
hidden states that cause them.”
之后可简化为
$ = \mathbb{E}_{q(s \mid o)} [\mathbb{E}_{q(o_{\tau} \mid \pi)}[ log q(o_{\tau} \mid \pi) – p(o_{\tau})]] – \mathbb{E}_{q(s \mid \pi)}[\mathbb{E}_{q(o_{\tau} \mid s_{\tau})} [log q(o_{\tau} \mid s_{\tau}) ]]$
$ -G_{\tau}(\pi) = \mathbb{E}_{q(s \mid o)} \left[ D[ q(o_{\tau} \mid \pi) || p(o_{\tau})] \right] + \mathbb{E}_{q(s \mid \pi)}[H(p(o_{\tau} \mid s_{\tau}))] $
第一项KL的预期,由于推断时s和o的一对一关系,简化为$D[ q(o_{\tau} \mid \pi) || p(o_{\tau} \mid m)]$,是根据prior belief $q(s)$计算出的posterior预测的o的分布与goal $p(o)$分布的差距,代表了产生偏离目标的结果的risk。
第二项代表了generative model的每一种s导致的o的熵(不确定性),在prior q下的预期。也可以解释为generative model中$p(o \mid s)$的模糊性。
一般这两者存在一个平衡取舍,当自由能固定不变时,可以理解为训练水平固定,推测得越肯定,就越可能产生不符合预期得结果,反之如果放宽结果使其比较模糊,那么就越不容易偏离直觉。
在推测时间上累积自由能
$G(\pi) = \sum\limits_{\tau>now} G_{\tau}(\pi)$
belief需要被更新,找到让积分最大化的$q(s)$,之后策略也可以被计算,产生action。
F和G的数学形式非常像,区别在于F定义了怎样的模型是当前时刻下一个好的推断,而G定义了一个目标,用于决定未来的actions u应该如何被计算。
active inference的过程可以大致理解为:
- o从环境采样
- 使用最近的策略$\pi$,求解能让F最大化的prior belief $q^*(s_{\tau}) = \arg\max_{q} F(o_{\tau}, q)$。
- 将$q^*(s)$带入expected free energy的计算,这里需要推测若干步直到step=T。每一步推测都需要在$\widetilde{q}(s)$的prior上,计算generative model的$p(s_t \mid o_t, s_{t-1}, s_{t+1})$,之后再计算有偏的$p(s_{1:T}, o_{1:T} \mid \pi, u_{1:T} ) $
- 使用softmax以及步骤3里获得的$p(s_{\tau:T}, o_{\tau:T})$,计算出EFE,也就是$G$,再计算出新的$\pi^{(G)}$。注意到G的计算中涉及到goal $p(o)$的设置
- 使用generative model计算$u_t = min_{u} \mathbb{E}_{q}[D[p(o_{t+1} \mid s_{t+1}) || R(o_{t+1} \mid s_{t}, u)]]$,需要prior belief 先给出$q(s+t)$和$q(s_{t+1})$,之后用transition model计算$s_{t+1}(s_{t}, u)$。凭感觉获得的$s_{t+1}$与根据模型推测的$s_{t+1}$会导致两个不同的$p(o \mid s)$,然后计算这两个的KL距离,选择最小KL的u作为action。总而言之就是选择与直觉的prior的推测结果导致的outcome最接近的一个action。
- 执行$u_{\tau}$,获得下一个step的o
generative model可以在一个probability graph内描述,包含了几个子模型:
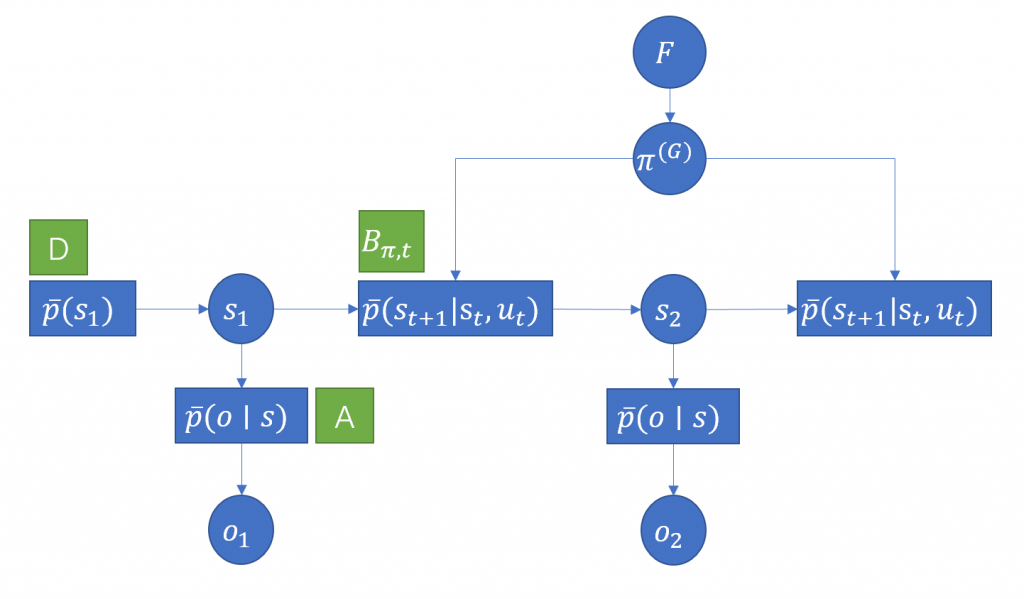
这里A、B、D都是推断模型,用operator的形态来代指模型推理。
论文中为了简化公式,用了一些规则符号:
省略log:$\hat{x} := log(x)$
粗体向量$\boldsymbol{x} := \left( q(s=0)x, q(s=1)x, … q(s=S)x \right)$,代表了x在$q(s)$下的后验。
s状态比较特殊,后验概率向量就是q,$\boldsymbol{s}=(q(s=0), q(s=1), … q(s=S))$
但计算$G$时要考虑策略的预期,于是
$\boldsymbol{s}_{\tau}^{\pi}$是$Pr(s)$以$q(s \mid \pi)$作为先验的,在第$\tau$时刻的后验预期,即$\boldsymbol{s}_{\tau}^{\pi} = \left( q(s_{\tau}=0 \mid \pi), q(s_{\tau}=1 \mid \pi), … \right)$。
所以$\boldsymbol{s}^{\pi}$需要用一个类似$Q(s, a)$的$S \times U$的矩阵来存储
考虑了策略后的s的预期概率是:$\boldsymbol{s}_t = \sum\limits_{u} \boldsymbol{\pi}(t, u) \cdot \boldsymbol{s}_{t}^{\pi}$
generative model里的概率矩阵A定义为$Pr(o=i \mid s=j) = A_{ij}$
于是$\boldsymbol{o} = A \boldsymbol{s} = \left( \mathbb{E}_{q(s)}[p(o=1, \mid s)], \mathbb{E}_{q(s)}[p(o=2, \mid s)], … \right)$,是离散o的后验。
generative model里的状态转移矩阵B定义为$P(s_{t+1}=i \mid s_t=j, \pi(t>0)) = B(u_t=\pi(t))_{ij}$
$\boldsymbol{s}_{\tau+1} = B_{\tau}^{\pi} \boldsymbol{s}_{\tau}^{\pi} $表示了转移到下一步之后的状态预期,计算时在所有u上进行了sum。
$\boldsymbol{s}_{t+1} = B(u) \boldsymbol{s}_t$则表示了当状态已经经过了策略预期后,如果选择action u,下一步的预期状态。
有了这些规则定义,再仔细看一下active inference的流程里的几个关键步骤计算:
- 已经有generative model,规划后续推理时,需要用到state estimation的方法: $\boldsymbol{s}_{\tau}^{\pi} = \sigma( \hat{A} o_{\tau} + \hat{B}_{\tau-1}^{\pi} \boldsymbol{s}_{\tau-1}^{\pi} + \hat{B}_{\tau+1}^{\pi} \boldsymbol{s}_{\tau+1}^{\pi})$ 根据概率图上,观测、前后两个时间的状态,分别计算各自推测的$\boldsymbol{s}_{\tau}^{\pi}$,之后取log相加,得到联合概率log,再用softmax归一化出一个$\boldsymbol{s}_{\tau}^{\pi}$。$o_{\tau}$这里不是向量,而是观测值,所以$Ao_{\tau}$是取A在输入的$o_{\tau}$下的slice的含义,而非矩阵x向量的操作。
- 计算$F$的方法:$-F = \boldsymbol{s}_{\tau}^{\pi} \cdot (\hat{\boldsymbol{s}}_{\tau}^{\pi} – \hat{B}_{\tau-1}^{\pi} \boldsymbol{s}_{\tau-1}^{\pi} – Ao_{\tau} )$,对照前面F转化为KL+A预期的形态。这里最外层的点乘执行了求预期的操作,最终获得每种u下的F值。优化$q(s \mid \pi)$时,选择$u_{t-1}$对应的一列作为loss。
- 计算$G$的方法:$-G(\pi, \tau) = \boldsymbol{o}_{\tau}^{\pi} \cdot (\hat{\boldsymbol{o}}_{\tau}^{\pi} – logp(o_{\tau})) – diag(A^T \hat{A}) \cdot \boldsymbol{s}_{\tau}^{\pi}$ 可以对照KL control转化后的$G$的公式,diag操作$A log A$矩阵后,得到的向量存储了每一种状态下,对应的outcome的熵。之后再计算了熵的后验预期。第一项代表了risk的KL距离里,$\boldsymbol{o}_{\tau}^{\pi} = A \boldsymbol{s}_{\tau}^{\pi}$,产生一个$O \times U$的矩阵。$p(o_{\tau})$则是我们的goal,需要用一个向量来描述每一种o对应的reward。
- policy计算时,累积$G(\pi, \tau)$然后在结果矩阵的不同u的axis上用softmax归一化。
- action选择:$u_t = min_{u} \boldsymbol{o}_{t+1} \cdot ( \hat{A} \boldsymbol{s}_{t+1} – \hat{A} B(u)\boldsymbol{s}_{t})$ 并非直接按概率从policy内greedy或是采样,这样会导致实际执行的action依旧倾向于最大化未来自由能预期。实际的action是略微“off-policy”的。首先通过G计算当前以及未来一步的策略,之后计算两步策略下的状态预期,当前步状态预期用转移矩阵推理一步后,产生的o,与下一步的状态直接产生的o,两者的KL距离最小的一种u才会被执行。所以我们会选择在增加最多自由能预期的策略下,最符合generative model的解释逻辑,产生的outcome最符合直觉的一种action。
